Mirror and Trans Tiles

The image of a tile under a shape conserving transform is also a tile. As reflections conserve shape this means that for all tiles there is a mirror image tile. (Except that dihedrally symmetric tiles are their own mirror images.)

Using the general form for an IFS, if a tile-generating IFS is

{ T_i: p → a_ip + v_i }

then the IFS for a mirror image is

{ T_i: p → a_ip + v_i }

In some cases tiles come in pairs, in one of which all elements are directly similar to the tile, and in the other of which all elements are inversely similar to the tile. From a loose analogy with chemistry terminology I call these cis- and trans- tiles respectively.

The IFS for a trans- tile, when all the elements have the same orientation, is

{ T_i: p → a_ip + v_i }

Note that for many of the more accessible tiles all the vectors are real (non-complex) or come in conjugate pairs. In this case conjugating the vectors is an unnecessary step.

Trans- tiles do not exist for all tiles not involving reflections. I don't have a general rule for identifying whether a particular tile has a trans- equivalent. However it can be seen that any rectangular tile is identical to its trans- tile. The existence of trans- tiles is common among rep-tiles.

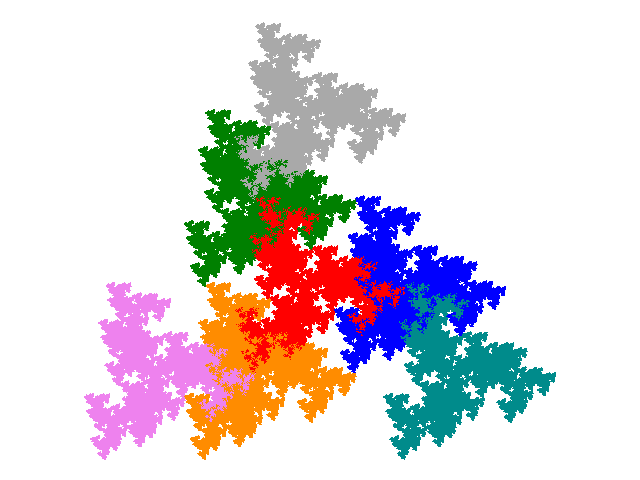
The (0-)spiral heptaheptals are used here as examples to illustrate mirror and trans- tiles. (The S-/Z- pentapletals would also have been a suitable example.)

The 0-spiral heptalheptal has the IFS { p → ap; p → ap + 1; p → ap + (√3i - 1)/2; p → ap - (√3i + 1)/2; p → ap + 1 - (√3i - 1)/2; p → ap + √3i; p → ap - 1 - (√3i + 1)/2 } and the attractor

Then its mirror image tile has the IFS { p → ap; p → ap + 1; p → ap - (√3i + 1)/2; p → ap + (√3i - 1)/2; p → ap + 1 + (√3i + 1)/2; p → ap - √3i; p → ap - 1 + (√3i - 1)/2 } and the attractor

The trans- versions of these have IFSs { p → ap̅; p → ap̅ + 1; p → ap̅ - (√3i + 1)/2; p → ap̅ + (√3i - 1)/2; p → ap̅ + 1 + (√3i + 1)/2; p → ap̅ - √3i; p → ap̅ - 1 + (√3i - 1)/2 } and { p → ap̅; p → ap̅ + 1; p → ap̅ + (√3i - 1)/2; p → ap̅ - (√3i + 1)/2; p → ap̅ + 1 - (√3i - 1)/2; p → ap̅ + √3i; p → ap̅ - 1 - (√3i + 1)/2 }.

Note that the mirror trans- tile has the same arrangement of elements as the cis-tile, and the mirror cis-tile the same arrangement of elements as the trans-tile.

The rule for the case when the elements don't all have the same orientation is complicated. The rule above seems to hold for linear trihextals, but the set of such tiles is sufficiently rich and dense (144 out of 216 combinations of orientations generate tiles) this might be coincidence. The rule also appears to hold for cyclic tetrahextals, but in this case the sets of cis- and trans- tiles are the same, so it could again be coincidence.

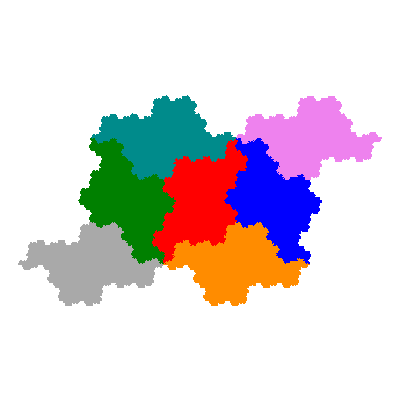
However the dragon heptahextal presents an instance in which the rule breaks down.

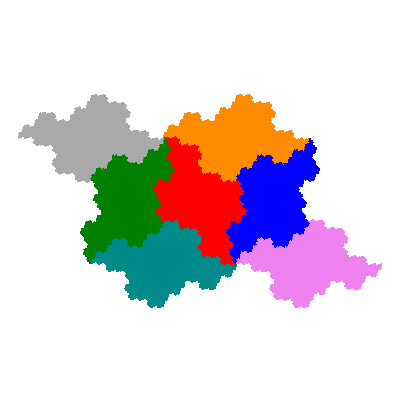
In this case it in necessary not only to mirrow the vector also to amend the angles. The IFS for the cis- tile is

{ p → e^iπ/3ap; p → e^iπ/6ap + 1; p → e^iπ/6ap - 1; p → ap + e_1,1; p → ap + e_-1,1; p → ap + e_-1,-1; p → ap + e_1,-1 }

and that for the trans- tile is

{ p → e^iπ/6ap; p → e^iπ/3ap + 1; p → e^iπ/3ap - 1; p → ap + e_1,1; p → ap + e_-1,1; p → ap + e_-1,-1; p → ap + e_1,-1 }

where e_i,j is an Eisenstein Integer. I don't have a proposed generalisation to cover this case.

It is possible that this explains why I haven't found any trans- tiles for cubic tiles - which always have elements with different orientations. It may be that the necessary adjustments to orientations are not compatible with the constraints on orientation for a cubic tile.

© 2016 Stewart R. Hinsley