
A construction for tiles with dissection equation nx + x2 + x3 (see there for tiling) produces an order 4 8th unit cubic Pisot tile, with dissection equation 2x + x2 + x3.

From this 4 order 7, 4 order 10 tiles, and 15 order 13 tiles can be derived.
There are 6 candidates for order 10 tiles, but two are disconnected, even though they do have a similarity dimension of 2, and tile the plane. There are two groups of candidates for order 13 tiles, one group of 4 being directly derived from the order 4 tile, and a second group of 28 derived indirectly via the order 7 tiles. However one of the first group, and 16 of the second group, are disconnected, although they again have a similarity dimension of 2, and tile the plane.
The order 7 tiles have dissection equations x + 3x2 + 2x3 + x4, 2x + 3x3 + x4 +x5, 2x + x2 + 2x4 + x5 + x6 and x + 3x2 + 2x3 + x4 (again).


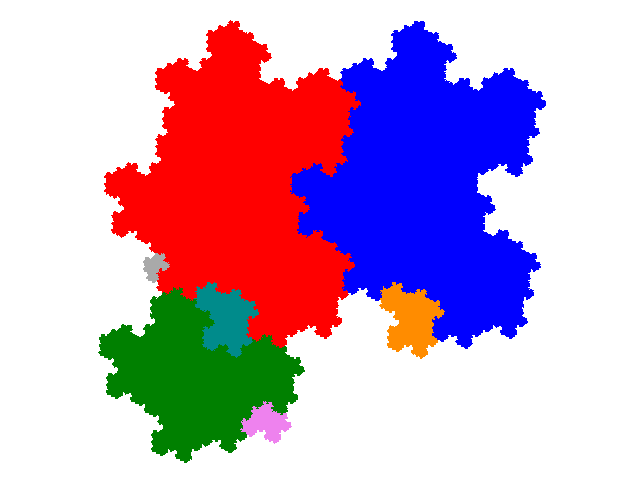
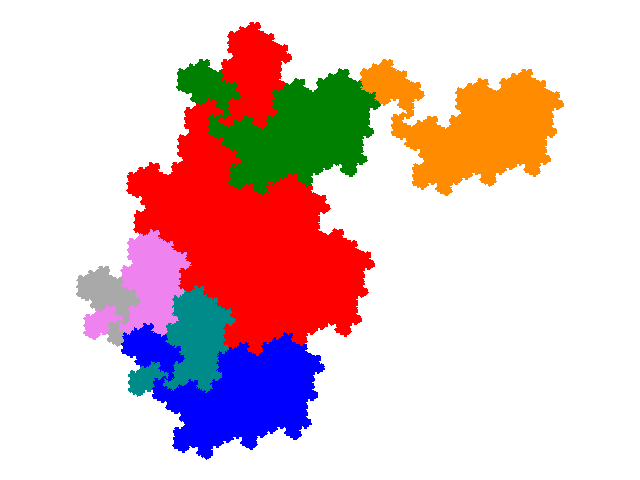
The order 10 tiles have dissection equations 2x + 2x3 + 3x4 + 2x5 + x6, x + 2x2 + 4x3 + 2x4 + x5, x + 3x2 + x3 + 3x4 + x5 + x6 and 5x2 + 3x3 + 2x4.




The first group of order 13 tiles contains the following.

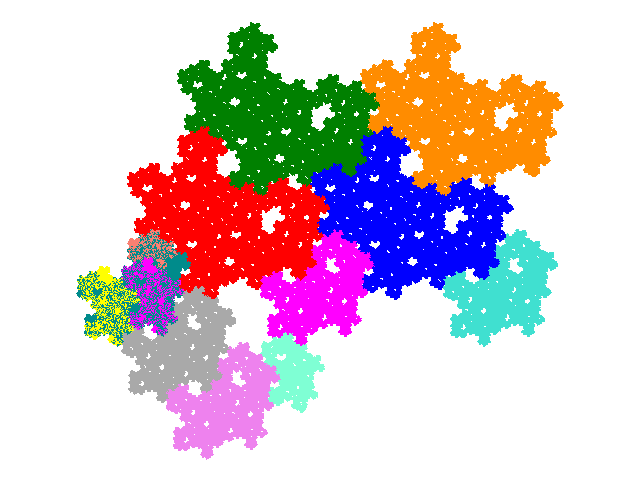

The second group of order 13 tiles contain the following.

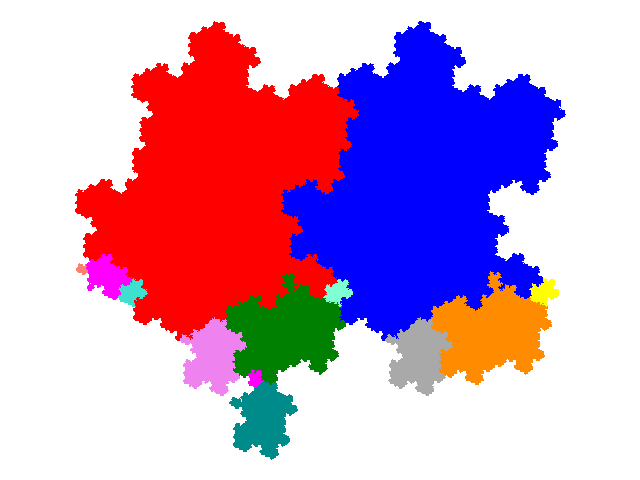










All of these figures tile the plane. The order 7 tiles have 2 copies in the unit cell, the order 10 tiles 3 copies in the unit cell, and the order 13 tiles 4 copies in the unit cell. The tiling vectors are the same as for the order 4 tile.













































© 2016 Stewart R. Hinsley