

In the case of fudgeflakes composition of appropriately scaled IFSs is a productive means of producing new tiles.
There are potentially 16 order 9 tiles generated from combinations of first order fudgeflakes (involving the cis- and trans- fudgeflakes and their mirror tiles). However a composition of an IFS with itself does not produce a new tile, but instead produces a higher order dissection of the original tile, and adding mirror tiles to the mix doesn't produce additional tiles (other than mirror tiles), instead generating the other tiles in the same and different orientations. Thus there are two novel order 9 tiles. If the cis-flowsnakes are denoted Fn and the trans-flowsnakes Fn then the order 9 tiles are F1.F1 and F1.F1.


Further tiles can be produced by composition of fudgeflakes of different orders, and by composition of composite fudgeflakes with fudgeflakes or other composite fudgeflakes. I have presumed that adding mirror tiles to the mix still doesn't generate further tiles, and haven't investigated their involvement further. Apart from this I conjecture that all cases generate tiles, and the only judgement necessary is to eliminate those which are higher order dissections of lower order tiles.
In addition to the 2 order 9 (32) tiles there are 6 order 27 (33) tiles, 8 order 36 (3×12) tiles, 20 order 81 (34 and 3×27) tiles, 24 order 108 (32×12) tiles, 10 order 144 (122 and 3×48) tiles, 8 order 225 (3×75) tiles, 30 order 243 (35) tiles, 40 order 324 (12×27 and 33×12) tiles, and so on.
The order 27 tiles are F1.F1.F1, F1.F1.F1, F1.F1.F1, F1.F1.F1, F1.F1.F1 and F1.F1.F1.






The order 36 tiles are F1.F2, F1.F2, F1.F2, F1.F2, F2.F1, F2.F1, F2.F1 and F2.F1







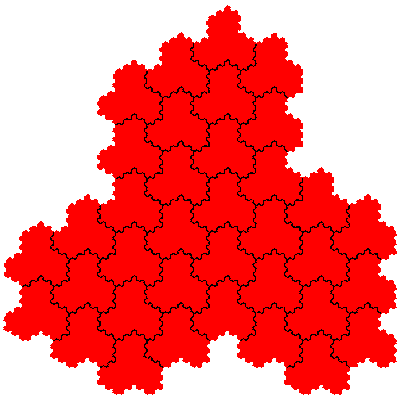
The order 81 tiles are F1.F1.F1.F1, F1.F1.F1.F1, F1.F1.F1.F1, F1.F1.F1.F1, F1.F1.F1.F1, F1.F1.F1.F1, F1.F1.F1.F1, F1.F1.F1.F1, F1.F1.F1.F1, F1.F1.F1.F1, F1.F1.F1.F1, F1.F1.F1.F1, F1.F2, F1.F2, F1.F2, F1.F2, F2.F1, F2.F1, F2.F1 and F2.F1.









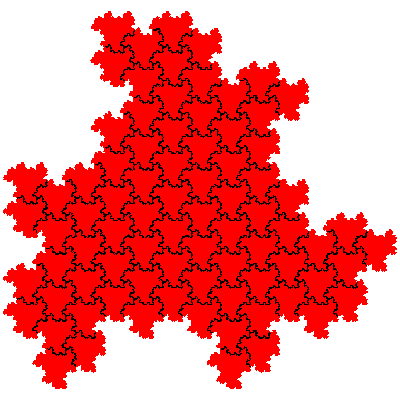





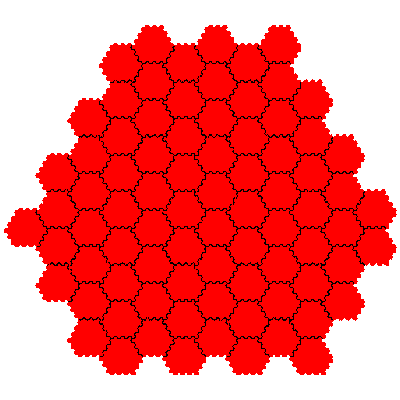




The order 108 tiles are F1.F1.F2, F1.F1.F2, F1.F1.F2, F1.F1.F2, F1.F1.F2, F1.F1.F2, F1.F1.F2, F1.F1.F2, F1.F2.F1, F1.F2.F1, F1.F2.F1, F1.F2.F1, F1.F2.F1, F1.F2.F1, F1.F2.F1, F1.F2.F1, F2.F1.F1, F2.F1.F1, F2.F1.F1, F2.F1.F1, F2.F1.F1, F2.F1.F1, F2.F1.F1 and F2.F1.F1.
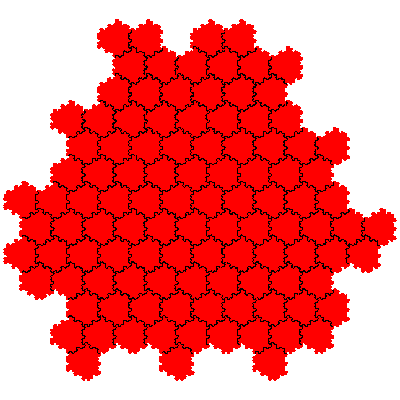

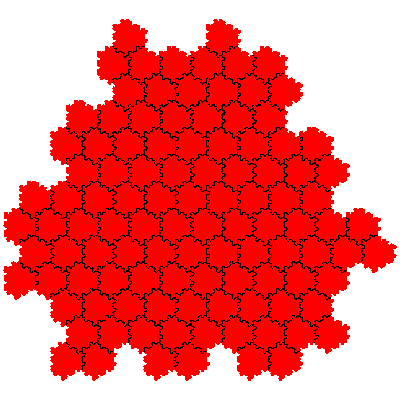
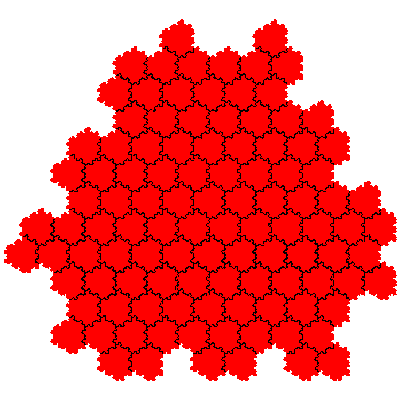












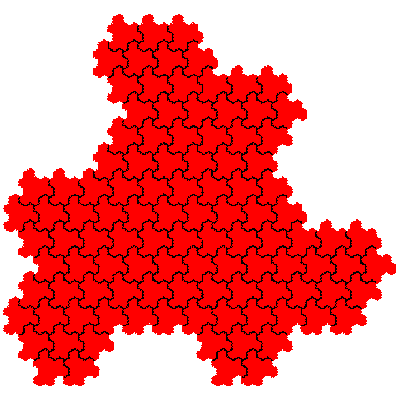
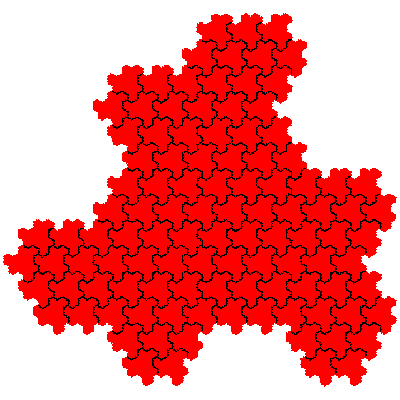


The order 144 tiles are F2.F2, F2.F2, F1.F4, F1.F4, F1.F4, F1.F4, F4.F1, F4.F1, F4.F1 and F4.F1.










The order 225 tiles are F1.F5, F1.F5, F1.F5, F1.F5, F5.F1, F5.F1, F5.F1 and F5.F1








The order 243 tiles are all combinations of 1st order fudgeflakes other than F1.F1.F1.F1.F1.F1 and F1.F1.F1.F1.F1.F1.
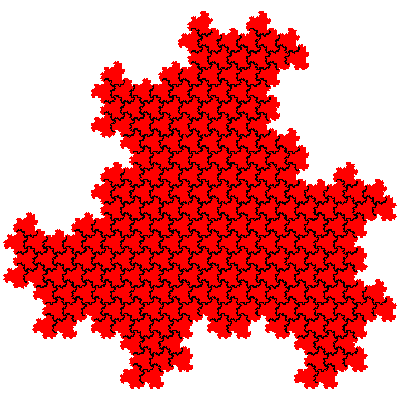

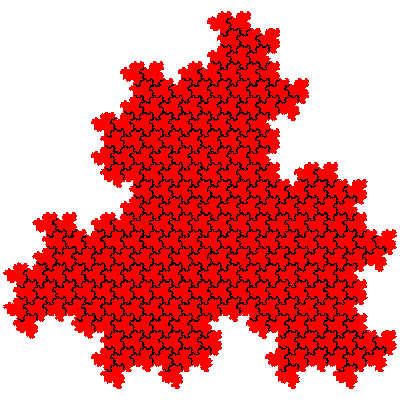

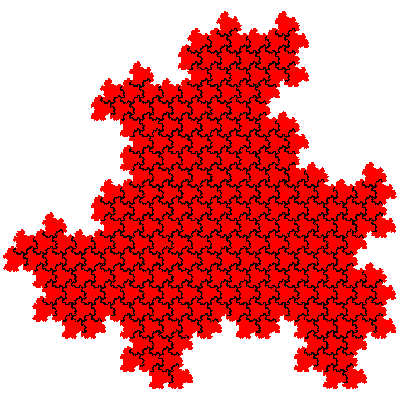


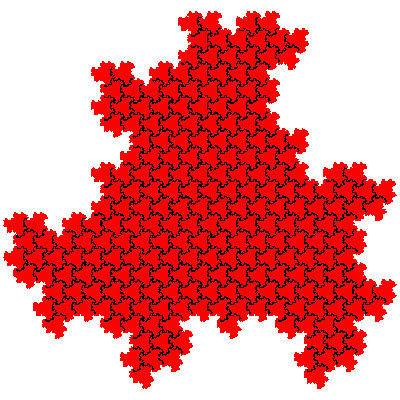




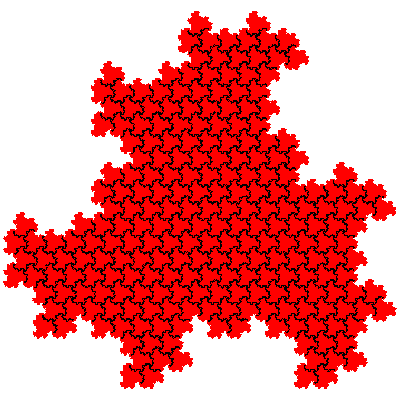

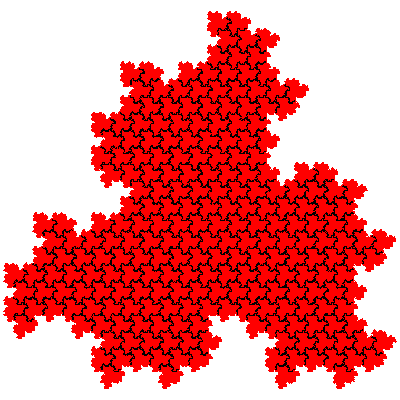

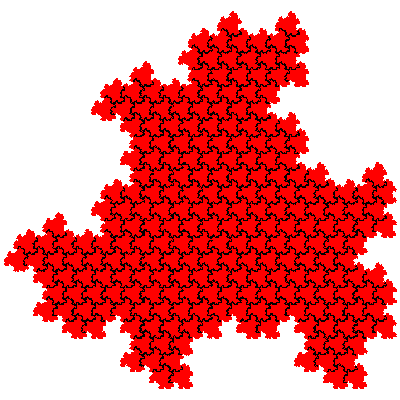
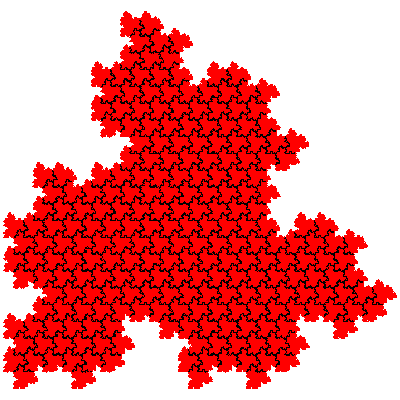


It is possible to calculate the number of tiles of particular orders based on 1st order fudgeflakes alone. When n 1st order fudgeflakes are combined there the resulting tiles have 3n elements. The number of IFSs is 2n (each element in the expression can be either the cis- or the trans- fudgeflake). From this number we have to subtract the number of IFSs which are composed solely of several copies of the same sequence of elements. When n is prime there are only two to remove - those corresponding to the cis- and trans-fudgeflakes. When n is composite we have to consider longer sequences. It is also sometimes necessary to add some back, to cater for the case when a sequence can be divided into equal parts in more than one way. e.g. F.F.F.F.F.F.F = (F.F.F).(F.F.F) = (F.F).(F.F).(F.F).
| compositional order | order (# of elements) of tile | number of tiles |
|---|---|---|
| 2 | 32 = 9 | 2 (22-2) |
| 3 | 33 = 27 | 6 (23-2) |
| 4 | 34 = 81 | 12 (24-22) |
| 5 | 35 = 243 | 30 (25-2) |
| 6 | 36 = 729 | 54 (26-23-22+2) |
| 7 | 37 = 2187 | 126 (27-2) |
| 8 | 38 = 6561 | 240 (28-24) |
| 9 | 39 = 19683 | 504 (29-23) |
| 10 | 310 = 59049 | 970 (210-25-22+2) |
| 11 | 311 = 177147 | 2046 (211-2) |
| 12 | 312 = 531441 | 4028 (212-26-24+22) |
| 13 | 313 = 1594323 | 8190 (213-2) |
| 14 | 314 = 4782969 | 16254 (214-27-22+2) |
| 15 | 315 = 14348907 | 32730 (215-25-23+2) |
There are 8 tiles based of compositional order 2 for each pair of fudgeflake orders. For tiles of compositional order 3 there are three cases, depending on whether 1, 2 or 3 fudgeflake orders are involved. The first is considered above. The second has 24 tiles (3 permutations of fudgeflake order x 23 selection of cis- versus trans- fudgeflakes), and the 3rd 48 tiles (6 permutations of fudgeflake order x 23 selection of cis- versus trans- fudgeflakes). Similar calculations can be performed for higher compositional orders, but in some cases one has to account for the generation of lower order tiles (e.g. F1.F2.F1.F2 does not generate a new tile).
© 2000, 2017 Stewart R. Hinsley