 rep-3 parallelogram
rep-3 parallelogram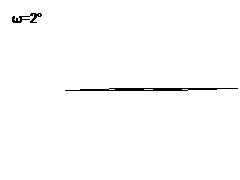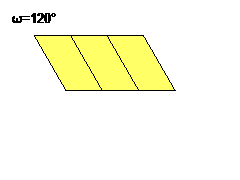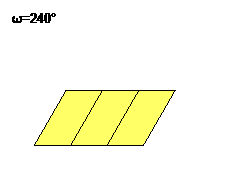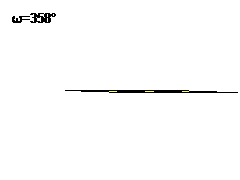 rep-4 parallelogram
rep-4 parallelogram rep-4 parallelogram
rep-4 parallelogram rep-6 parallelogram
rep-6 parallelogram
In some ways parallelograms are among the least interesting of self-similar tiles. A single construction generates all parallelograms as order 4 rep-tiles (which are Perron tiles) which tile the plane with a single copy in the unit cell, and one might consider this sufficient.
However there are 3 parallelograms which have lower order. The √2:1 rectangle is an order 2 Perron rep-tile, the √3:1 rectangle is an order 3 Perron rep-tile, and the golden rectangle is an order 3 Perron irrep-tile. The corresponding parallelograms are pseudo-Perron tiles.
All of these are the lowest order members of larger classes of contructions: the order 4 tiles of the rep-n2-parallograms, √2:1 rectangle and √3:1 rectangles of the rep-mn-parallelograms, and the golden tile of the metallic parallelograms.
There are many other ways of dissecting parallelograms into similar parallelograms. A subset of these, in which a square of integer side is dissected into smaller squares also of integer side have been investigated at Erich Friedman's Math Magic pages. (When generalised to parallelograms these these become ir-reptiles with IFS { p →ki/np + vi : ki, n ∈ ℤ}.) They lose the property that sides are of integer size (except from rhombi), but the ratio of areas remains the ratio of a pair of integer squares.)
Any parallelogram is a rep-n2 rep-tile, and tiles the plane with one copy per unit cell.
Specific classes of parallelograms are squares (all angles and sides equal), rectangles (all angles equal) and rhombi (all sides equal). Several classes of polyforms include parallelograms, including polyominos, polyplets, polyabolos (aka polytans), polyiamonds and polydrafters.
| square (monomino) |
|||||
| rectangle (domino) |
|||||
| rhombus (diamond) |
|||||
| parallelogram (diabolo) |
|||||
| parallelogram (didrafter) |
In the simplest construction of these figures all the transforms are n-fold contractions combined with translations. This may be written
Trs: p → p/n + ra + sb, r,s ∈0..n-1, where a and b are non-colinear vectors.
These IFSs have two degrees of freedom, which means that their attractors include an uncountably infinite number of dissimilar parallelograms. The degrees of freedom may be parameterised as stretch and skew. If the archetypal IFS is made that of the square with a = 1 and b = i, then the generalised IFS can be written as a = t and b = k + i, i.e.
Trs: p → p/n + rt + sk + si, r,s ∈0..n-1
However, because of the symmetry of the attractors, the attractors are degenerate, i.e. any particular parallelogram can be produced by more than one IFS. In all cases any element of the parallelogram may be rotated by 180°, giving 2n2 different IFSs. In the case of rectangles and rhombi any element may be reflected in either or both of two axes, giving 4n2 different IFSs. (Reflection in both axes is the same as rotation by 180°.) In the case of squares any element may also be rotated by 90° or 270°, instead of 0° or 180°, giving 8n2 different IFSs.
Furthermore some particular figures have additional IFSs; for example in the domino pairs of elements form a square, and any or all these can collectively by rotated by 90°. Thus the rep-4 domino is 16384 (4.84) rather than 4096 (84) -fold degenerate.
This degeneracy becomes significant when applying various algorithmic methods of generating new reptiles and irreptiles from a given reptile or irreptile.
There are also rep-mn rectangles, including two with rep- numbers less than 4.
| rep-n rectangle |
√2:1 (rep-2) rectangle |
√3:1 (rep-3) rectangle |
2:1 (rep-4) rectangle |
√5:1 (rep-5) rectangle |
√6:1 (rep-6) rectangle |
| rep-2n rectangle |
(rep-4) square |
√3:√2 (rep-6) rectangle |
√2:1 (rep-8) rectangle |
√5:√2 (rep-10) rectangle |
√3:1 (rep-12) rectangle |
| rep-3n rectangle |
√3:√2 (rep-6) rectangle |
(rep-9) square |
2:√3 (rep-12) rectangle |
√5:√3 (rep-15) rectangle |
√2:1 (rep-18) rectangle |
| rep-4n rectangle |
2:1 (rep-8) rectangle |
2:√3 (rep-12) rectangle |
(rep-16) square |
√5:√4 (rep-20) rectangle |
√3:√2 (rep-24) rectangle |
The rep-nn rectangle is square (one of the degenerate alternatives to the rep-n2 square above). The rep-nm rectangle is the same as the rep-mn rectangle, but rotated by 90°.
The simplest construction is a combination of an anticlockwise rotation by 90°, combined with contraction by √(mn) and a translation, which may be written as
Trs: p → peiπ/2/√(mn) + r1 + (s-1)√(m/n)i, r ∈1..n, s ∈1..m, where 1 and i are orthogonal unit vectors.
These IFSs have no degrees of freedom, their attractors being the √n:m rectangles. These can be placed in a one-to-one correspondence with the rational numbers (m/n), and hence form a countably infinite set of attractors.
Rep-mn rectangles are in general 4mn degenerate. Some specific instances (e.g. square and domino - see above) have greater degrees of degeneracy.
The √n:m rectangles can also be generated by a combination of reflection in the x-axis, anticlockwise rotation by 90°, contraction by √(mn) and a translation, which may be written as
Trs: p → p̄eiπ/2/√(mn) + (r-1)1 + (s-1)√(m/n)i, r ∈1..n, s ∈1..m, where 1 and i are orthogonal unit vectors.
| rep-n rectangle |
√2:1 (rep-2) rectangle |
√3:1 (rep-3) rectangle |
2:1 (rep-4) rectangle |
√5:1 (rep-5) rectangle |
√6:1 (rep-6) rectangle |
| rep-2n rectangle |
(rep-4) square |
√3:2 (rep-6) rectangle |
√2:1 (rep-8) rectangle |
√5:2 (rep-10) rectangle |
√3:1 (rep-12) rectangle |
| rep-3n rectangle |
√3:2 (rep-6) rectangle |
(rep-9) square |
3:2 (rep-12) rectangle |
√5:3 (rep-15) rectangle |
√6:3 (rep-18) rectangle |
These are a special case of the rep-mn parallelograms, which are sets of attractors with a single degree of freedom, which can be parameterised as the angle of the lower left corner. The IFS transforms then become
Trs: p → p̄eω/2/√(mn) + (r-1)1 + (s-1)√(m/n)i, r ∈1..n, s ∈1..m, where 1 and i are orthogonal unit vectors.
rep-2 parallelogram rep-3 parallelogram
rep-3 parallelogram rep-4 parallelogram
rep-4 parallelogram rep-4 parallelogram
rep-4 parallelogram rep-6 parallelogram
rep-6 parallelogram
It is also possible to generate rectangles composed of alternating columns (or rows) of rotated and unrotated elements.
11121,1,1,2 1.4142135623731 11131,1,1,3 1.2247448713916 11141,1,1,4 1.1547005383793 11151,1,1,5 1.1180339887499 11161,1,1,6 1.0954451150103 11171,1,1,7 1.0801234497346 11181,1,1,8 1.0690449676497 11231,1,2,3 1.7320508075689 11241,1,2,4 1.4142135623731 11251,1,2,5 1.2909944487358 11261,1,2,6 1.2247448713916 11271,1,2,7 1.1832159566199 11281,1,2,8 1.1547005383793 11341,1,3,4 2 11351,1,3,5 1.5811388300842 11361,1,3,6 1.4142135623731 11371,1,3,7 1.3228756555323 11381,1,3,8 1.2649110640674 11451,1,4,5 2.2360679774998 11461,1,4,6 1.7320508075689 11471,1,4,7 1.5275252316519 11481,1,4,8 1.4142135623731 11561,1,5,6 2.4494897427832 11571,1,5,7 1.870828693387 11581,1,5,8 1.6329931618555 11671,1,6,7 2.6457513110646 11681,1,6,8 2 11781,1,7,8 2.8284271247462 12121,2,1,2 1 12131,2,1,3 0.86602540378444 12141,2,1,4 0.81649658092773 12151,2,1,5 0.79056941504209 12161,2,1,6 0.77459666924148 12171,2,1,7 0.76376261582597 12181,2,1,8 0.75592894601845 12231,2,2,3 1.2247448713916 12241,2,2,4 1 12251,2,2,5 0.91287092917528 12261,2,2,6 0.86602540378444 12271,2,2,7 0.83666002653408 12281,2,2,8 0.81649658092773 12341,2,3,4 1.4142135623731 12351,2,3,5 1.1180339887499 12361,2,3,6 1 12371,2,3,7 0.93541434669349 12381,2,3,8 0.89442719099992 12451,2,4,5 1.5811388300842 12461,2,4,6 1.2247448713916 12471,2,4,7 1.0801234497346 12481,2,4,8 1 12561,2,5,6 1.7320508075689 12571,2,5,7 1.3228756555323 12581,2,5,8 1.1547005383793 12671,2,6,7 1.870828693387 12681,2,6,8 1.4142135623731 12781,2,7,8 2 13121,3,1,2 0.81649658092773 13131,3,1,3 0.70710678118655 13141,3,1,4 0.66666666666667 13151,3,1,5 0.6454972243679 13161,3,1,6 0.63245553203368 13171,3,1,7 0.62360956446232 13181,3,1,8 0.61721339984837 13231,3,2,3 1 13241,3,2,4 0.81649658092773 13251,3,2,5 0.74535599249993 13261,3,2,6 0.70710678118655 13271,3,2,7 0.68313005106397 13281,3,2,8 0.66666666666667 13341,3,3,4 1.1547005383793 13351,3,3,5 0.91287092917528 13361,3,3,6 0.81649658092773 13371,3,3,7 0.76376261582597 13381,3,3,8 0.73029674334022 13451,3,4,5 1.2909944487358 13461,3,4,6 1 13471,3,4,7 0.8819171036882 13481,3,4,8 0.81649658092773 13561,3,5,6 1.4142135623731 13571,3,5,7 1.0801234497346 13581,3,5,8 0.94280904158206 13671,3,6,7 1.5275252316519 13681,3,6,8 1.1547005383793 13781,3,7,8 1.6329931618555 14121,4,1,2 0.70710678118655 14131,4,1,3 0.61237243569579 14141,4,1,4 0.57735026918963 14151,4,1,5 0.55901699437495 14161,4,1,6 0.54772255750517 14171,4,1,7 0.54006172486732 14181,4,1,8 0.53452248382485 14231,4,2,3 0.86602540378444 14241,4,2,4 0.70710678118655 14251,4,2,5 0.6454972243679 14261,4,2,6 0.61237243569579 14271,4,2,7 0.59160797830996 14281,4,2,8 0.57735026918963 14341,4,3,4 1 14351,4,3,5 0.79056941504209 14361,4,3,6 0.70710678118655 14371,4,3,7 0.66143782776615 14381,4,3,8 0.63245553203368 14451,4,4,5 1.1180339887499 14461,4,4,6 0.86602540378444 14471,4,4,7 0.76376261582597 14481,4,4,8 0.70710678118655 14561,4,5,6 1.2247448713916 14571,4,5,7 0.93541434669349 14581,4,5,8 0.81649658092773 14671,4,6,7 1.3228756555323 14681,4,6,8 1 14781,4,7,8 1.4142135623731 15121,5,1,2 0.63245553203368 15131,5,1,3 0.54772255750517 15141,5,1,4 0.51639777949432 15151,5,1,5 0.5 15161,5,1,6 0.48989794855664 15171,5,1,7 0.48304589153965 15181,5,1,8 0.47809144373376 15231,5,2,3 0.77459666924148 15241,5,2,4 0.63245553203368 15251,5,2,5 0.57735026918963 15261,5,2,6 0.54772255750517 15271,5,2,7 0.52915026221292 15281,5,2,8 0.51639777949432 15341,5,3,4 0.89442719099992 15351,5,3,5 0.70710678118655 15361,5,3,6 0.63245553203368 15371,5,3,7 0.59160797830996 15381,5,3,8 0.56568542494924 15451,5,4,5 1 15461,5,4,6 0.77459666924148 15471,5,4,7 0.68313005106397 15481,5,4,8 0.63245553203368 15561,5,5,6 1.0954451150103 15571,5,5,7 0.83666002653408 15581,5,5,8 0.73029674334022 15671,5,6,7 1.1832159566199 15681,5,6,8 0.89442719099992 15781,5,7,8 1.2649110640674 16121,6,1,2 0.57735026918963 16131,6,1,3 0.5 16141,6,1,4 0.47140452079103 16151,6,1,5 0.45643546458764 16161,6,1,6 0.44721359549996 16171,6,1,7 0.4409585518441 16181,6,1,8 0.43643578047198 16231,6,2,3 0.70710678118655 16241,6,2,4 0.57735026918963 16251,6,2,5 0.52704627669473 16261,6,2,6 0.5 16271,6,2,7 0.48304589153965 16281,6,2,8 0.47140452079103 16341,6,3,4 0.81649658092773 16351,6,3,5 0.6454972243679 16361,6,3,6 0.57735026918963 16371,6,3,7 0.54006172486732 16381,6,3,8 0.51639777949432 16451,6,4,5 0.91287092917528 16461,6,4,6 0.70710678118655 16471,6,4,7 0.62360956446232 16481,6,4,8 0.57735026918963 16561,6,5,6 1 16571,6,5,7 0.76376261582597 16581,6,5,8 0.66666666666667 16671,6,6,7 1.0801234497346 16681,6,6,8 0.81649658092773 16781,6,7,8 1.1547005383793 17121,7,1,2 0.53452248382485 17131,7,1,3 0.46291004988628 17141,7,1,4 0.43643578047198 17151,7,1,5 0.42257712736426 17161,7,1,6 0.41403933560541 17171,7,1,7 0.40824829046386 17181,7,1,8 0.40406101782088 17231,7,2,3 0.65465367070798 17241,7,2,4 0.53452248382485 17251,7,2,5 0.48795003647427 17261,7,2,6 0.46291004988628 17271,7,2,7 0.44721359549996 17281,7,2,8 0.43643578047198 17341,7,3,4 0.75592894601845 17351,7,3,5 0.5976143046672 17361,7,3,6 0.53452248382485 17371,7,3,7 0.5 17381,7,3,8 0.47809144373376 17451,7,4,5 0.84515425472852 17461,7,4,6 0.65465367070798 17471,7,4,7 0.57735026918963 17481,7,4,8 0.53452248382485 17561,7,5,6 0.92582009977255 17571,7,5,7 0.70710678118655 17581,7,5,8 0.61721339984837 17671,7,6,7 1 17681,7,6,8 0.75592894601845 17781,7,7,8 1.0690449676497 18121,8,1,2 0.5 18131,8,1,3 0.43301270189222 18141,8,1,4 0.40824829046386 18151,8,1,5 0.39528470752105 18161,8,1,6 0.38729833462074 18171,8,1,7 0.38188130791299 18181,8,1,8 0.37796447300923 18231,8,2,3 0.61237243569579 18241,8,2,4 0.5 18251,8,2,5 0.45643546458764 18261,8,2,6 0.43301270189222 18271,8,2,7 0.41833001326704 18281,8,2,8 0.40824829046386 18341,8,3,4 0.70710678118655 18351,8,3,5 0.55901699437495 18361,8,3,6 0.5 18371,8,3,7 0.46770717334674 18381,8,3,8 0.44721359549996 18451,8,4,5 0.79056941504209 18461,8,4,6 0.61237243569579 18471,8,4,7 0.54006172486732 18481,8,4,8 0.5 18561,8,5,6 0.86602540378444 18571,8,5,7 0.66143782776615 18581,8,5,8 0.57735026918963 18671,8,6,7 0.93541434669349 18681,8,6,8 0.70710678118655 18781,8,7,8 1 21122,1,1,2 2 21132,1,1,3 1.7320508075689 21142,1,1,4 1.6329931618555 21152,1,1,5 1.5811388300842 21162,1,1,6 1.549193338483 21172,1,1,7 1.5275252316519 21182,1,1,8 1.5118578920369 21232,1,2,3 2.4494897427832 21242,1,2,4 2 21252,1,2,5 1.8257418583506 21262,1,2,6 1.7320508075689 21272,1,2,7 1.6733200530682 21282,1,2,8 1.6329931618555 21342,1,3,4 2.8284271247462 21352,1,3,5 2.2360679774998 21362,1,3,6 2 21372,1,3,7 1.870828693387 21382,1,3,8 1.7888543819998 21452,1,4,5 3.1622776601684 21462,1,4,6 2.4494897427832 21472,1,4,7 2.1602468994693 21482,1,4,8 2 21562,1,5,6 3.4641016151378 21572,1,5,7 2.6457513110646 21582,1,5,8 2.3094010767585 21672,1,6,7 3.7416573867739 21682,1,6,8 2.8284271247462 21782,1,7,8 4 22122,2,1,2 1.4142135623731 22132,2,1,3 1.2247448713916 22142,2,1,4 1.1547005383793 22152,2,1,5 1.1180339887499 22162,2,1,6 1.0954451150103 22172,2,1,7 1.0801234497346 22182,2,1,8 1.0690449676497 22232,2,2,3 1.7320508075689 22242,2,2,4 1.4142135623731 22252,2,2,5 1.2909944487358 22262,2,2,6 1.2247448713916 22272,2,2,7 1.1832159566199 22282,2,2,8 1.1547005383793 22342,2,3,4 2 22352,2,3,5 1.5811388300842 22362,2,3,6 1.4142135623731 22372,2,3,7 1.3228756555323 22382,2,3,8 1.2649110640674 22452,2,4,5 2.2360679774998 22462,2,4,6 1.7320508075689 22472,2,4,7 1.5275252316519 22482,2,4,8 1.4142135623731 22562,2,5,6 2.4494897427832 22572,2,5,7 1.870828693387 22582,2,5,8 1.6329931618555 22672,2,6,7 2.6457513110646 22682,2,6,8 2 22782,2,7,8 2.8284271247462 23122,3,1,2 1.1547005383793 23132,3,1,3 1 23142,3,1,4 0.94280904158206 23152,3,1,5 0.91287092917528 23162,3,1,6 0.89442719099992 23172,3,1,7 0.8819171036882 23182,3,1,8 0.87287156094397 23232,3,2,3 1.4142135623731 23242,3,2,4 1.1547005383793 23252,3,2,5 1.0540925533895 23262,3,2,6 1 23272,3,2,7 0.9660917830793 23282,3,2,8 0.94280904158206 23342,3,3,4 1.6329931618555 23352,3,3,5 1.2909944487358 23362,3,3,6 1.1547005383793 23372,3,3,7 1.0801234497346 23382,3,3,8 1.0327955589886 23452,3,4,5 1.8257418583506 23462,3,4,6 1.4142135623731 23472,3,4,7 1.2472191289246 23482,3,4,8 1.1547005383793 23562,3,5,6 2 23572,3,5,7 1.5275252316519 23582,3,5,8 1.3333333333333 23672,3,6,7 2.1602468994693 23682,3,6,8 1.6329931618555 23782,3,7,8 2.3094010767585 24122,4,1,2 1 24132,4,1,3 0.86602540378444 24142,4,1,4 0.81649658092773 24152,4,1,5 0.79056941504209 24162,4,1,6 0.77459666924148 24172,4,1,7 0.76376261582597 24182,4,1,8 0.75592894601845 24232,4,2,3 1.2247448713916 24242,4,2,4 1 24252,4,2,5 0.91287092917528 24262,4,2,6 0.86602540378444 24272,4,2,7 0.83666002653408 24282,4,2,8 0.81649658092773 24342,4,3,4 1.4142135623731 24352,4,3,5 1.1180339887499 24362,4,3,6 1 24372,4,3,7 0.93541434669349 24382,4,3,8 0.89442719099992 24452,4,4,5 1.5811388300842 24462,4,4,6 1.2247448713916 24472,4,4,7 1.0801234497346 24482,4,4,8 1 24562,4,5,6 1.7320508075689 24572,4,5,7 1.3228756555323 24582,4,5,8 1.1547005383793 24672,4,6,7 1.870828693387 24682,4,6,8 1.4142135623731 24782,4,7,8 2 25122,5,1,2 0.89442719099992 25132,5,1,3 0.77459666924148 25142,5,1,4 0.73029674334022 25152,5,1,5 0.70710678118655 25162,5,1,6 0.69282032302755 25172,5,1,7 0.68313005106397 25182,5,1,8 0.67612340378281 25232,5,2,3 1.0954451150103 25242,5,2,4 0.89442719099992 25252,5,2,5 0.81649658092773 25262,5,2,6 0.77459666924148 25272,5,2,7 0.74833147735479 25282,5,2,8 0.73029674334022 25342,5,3,4 1.2649110640674 25352,5,3,5 1 25362,5,3,6 0.89442719099992 25372,5,3,7 0.83666002653408 25382,5,3,8 0.8 25452,5,4,5 1.4142135623731 25462,5,4,6 1.0954451150103 25472,5,4,7 0.9660917830793 25482,5,4,8 0.89442719099992 25562,5,5,6 1.549193338483 25572,5,5,7 1.1832159566199 25582,5,5,8 1.0327955589886 25672,5,6,7 1.6733200530682 25682,5,6,8 1.2649110640674 25782,5,7,8 1.7888543819998 26122,6,1,2 0.81649658092773 26132,6,1,3 0.70710678118655 26142,6,1,4 0.66666666666667 26152,6,1,5 0.6454972243679 26162,6,1,6 0.63245553203368 26172,6,1,7 0.62360956446232 26182,6,1,8 0.61721339984837 26232,6,2,3 1 26242,6,2,4 0.81649658092773 26252,6,2,5 0.74535599249993 26262,6,2,6 0.70710678118655 26272,6,2,7 0.68313005106397 26282,6,2,8 0.66666666666667 26342,6,3,4 1.1547005383793 26352,6,3,5 0.91287092917528 26362,6,3,6 0.81649658092773 26372,6,3,7 0.76376261582597 26382,6,3,8 0.73029674334022 26452,6,4,5 1.2909944487358 26462,6,4,6 1 26472,6,4,7 0.8819171036882 26482,6,4,8 0.81649658092773 26562,6,5,6 1.4142135623731 26572,6,5,7 1.0801234497346 26582,6,5,8 0.94280904158206 26672,6,6,7 1.5275252316519 26682,6,6,8 1.1547005383793 26782,6,7,8 1.6329931618555 27122,7,1,2 0.75592894601845 27132,7,1,3 0.65465367070798 27142,7,1,4 0.61721339984837 27152,7,1,5 0.5976143046672 27162,7,1,6 0.58554004376912 27172,7,1,7 0.57735026918963 27182,7,1,8 0.57142857142857 27232,7,2,3 0.92582009977255 27242,7,2,4 0.75592894601845 27252,7,2,5 0.69006555934235 27262,7,2,6 0.65465367070798 27272,7,2,7 0.63245553203368 27282,7,2,8 0.61721339984837 27342,7,3,4 1.0690449676497 27352,7,3,5 0.84515425472852 27362,7,3,6 0.75592894601845 27372,7,3,7 0.70710678118655 27382,7,3,8 0.67612340378281 27452,7,4,5 1.1952286093344 27462,7,4,6 0.92582009977255 27472,7,4,7 0.81649658092773 27482,7,4,8 0.75592894601845 27562,7,5,6 1.309307341416 27572,7,5,7 1 27582,7,5,8 0.87287156094397 27672,7,6,7 1.4142135623731 27682,7,6,8 1.0690449676497 27782,7,7,8 1.5118578920369 28122,8,1,2 0.70710678118655 28132,8,1,3 0.61237243569579 28142,8,1,4 0.57735026918963 28152,8,1,5 0.55901699437495 28162,8,1,6 0.54772255750517 28172,8,1,7 0.54006172486732 28182,8,1,8 0.53452248382485 28232,8,2,3 0.86602540378444 28242,8,2,4 0.70710678118655 28252,8,2,5 0.6454972243679 28262,8,2,6 0.61237243569579 28272,8,2,7 0.59160797830996 28282,8,2,8 0.57735026918963 28342,8,3,4 1 28352,8,3,5 0.79056941504209 28362,8,3,6 0.70710678118655 28372,8,3,7 0.66143782776615 28382,8,3,8 0.63245553203368 28452,8,4,5 1.1180339887499 28462,8,4,6 0.86602540378444 28472,8,4,7 0.76376261582597 28482,8,4,8 0.70710678118655 28562,8,5,6 1.2247448713916 28572,8,5,7 0.93541434669349 28582,8,5,8 0.81649658092773 28672,8,6,7 1.3228756555323 28682,8,6,8 1 28782,8,7,8 1.4142135623731 31123,1,1,2 2.4494897427832 31133,1,1,3 2.1213203435596 31143,1,1,4 2 31153,1,1,5 1.9364916731037 31163,1,1,6 1.897366596101 31173,1,1,7 1.870828693387 31183,1,1,8 1.8516401995451 31233,1,2,3 3 31243,1,2,4 2.4494897427832 31253,1,2,5 2.2360679774998 31263,1,2,6 2.1213203435596 31273,1,2,7 2.0493901531919 31283,1,2,8 2 31343,1,3,4 3.4641016151378 31353,1,3,5 2.7386127875258 31363,1,3,6 2.4494897427832 31373,1,3,7 2.2912878474779 31383,1,3,8 2.1908902300207 31453,1,4,5 3.8729833462074 31463,1,4,6 3 31473,1,4,7 2.6457513110646 31483,1,4,8 2.4494897427832 31563,1,5,6 4.2426406871193 31573,1,5,7 3.2403703492039 31583,1,5,8 2.8284271247462 31673,1,6,7 4.5825756949558 31683,1,6,8 3.4641016151378 31783,1,7,8 4.8989794855664 32123,2,1,2 1.7320508075689 32133,2,1,3 1.5 32143,2,1,4 1.4142135623731 32153,2,1,5 1.3693063937629 32163,2,1,6 1.3416407864999 32173,2,1,7 1.3228756555323 32183,2,1,8 1.309307341416 32233,2,2,3 2.1213203435596 32243,2,2,4 1.7320508075689 32253,2,2,5 1.5811388300842 32263,2,2,6 1.5 32273,2,2,7 1.4491376746189 32283,2,2,8 1.4142135623731 32343,2,3,4 2.4494897427832 32353,2,3,5 1.9364916731037 32363,2,3,6 1.7320508075689 32373,2,3,7 1.620185174602 32383,2,3,8 1.549193338483 32453,2,4,5 2.7386127875258 32463,2,4,6 2.1213203435596 32473,2,4,7 1.870828693387 32483,2,4,8 1.7320508075689 32563,2,5,6 3 32573,2,5,7 2.2912878474779 32583,2,5,8 2 32673,2,6,7 3.2403703492039 32683,2,6,8 2.4494897427832 32783,2,7,8 3.4641016151378 33123,3,1,2 1.4142135623731 33133,3,1,3 1.2247448713916 33143,3,1,4 1.1547005383793 33153,3,1,5 1.1180339887499 33163,3,1,6 1.0954451150103 33173,3,1,7 1.0801234497346 33183,3,1,8 1.0690449676497 33233,3,2,3 1.7320508075689 33243,3,2,4 1.4142135623731 33253,3,2,5 1.2909944487358 33263,3,2,6 1.2247448713916 33273,3,2,7 1.1832159566199 33283,3,2,8 1.1547005383793 33343,3,3,4 2 33353,3,3,5 1.5811388300842 33363,3,3,6 1.4142135623731 33373,3,3,7 1.3228756555323 33383,3,3,8 1.2649110640674 33453,3,4,5 2.2360679774998 33463,3,4,6 1.7320508075689 33473,3,4,7 1.5275252316519 33483,3,4,8 1.4142135623731 33563,3,5,6 2.4494897427832 33573,3,5,7 1.870828693387 33583,3,5,8 1.6329931618555 33673,3,6,7 2.6457513110646 33683,3,6,8 2 33783,3,7,8 2.8284271247462 34123,4,1,2 1.2247448713916 34133,4,1,3 1.0606601717798 34143,4,1,4 1 34153,4,1,5 0.96824583655185 34163,4,1,6 0.94868329805051 34173,4,1,7 0.93541434669349 34183,4,1,8 0.92582009977255 34233,4,2,3 1.5 34243,4,2,4 1.2247448713916 34253,4,2,5 1.1180339887499 34263,4,2,6 1.0606601717798 34273,4,2,7 1.024695076596 34283,4,2,8 1 34343,4,3,4 1.7320508075689 34353,4,3,5 1.3693063937629 34363,4,3,6 1.2247448713916 34373,4,3,7 1.145643923739 34383,4,3,8 1.0954451150103 34453,4,4,5 1.9364916731037 34463,4,4,6 1.5 34473,4,4,7 1.3228756555323 34483,4,4,8 1.2247448713916 34563,4,5,6 2.1213203435596 34573,4,5,7 1.620185174602 34583,4,5,8 1.4142135623731 34673,4,6,7 2.2912878474779 34683,4,6,8 1.7320508075689 34783,4,7,8 2.4494897427832 35123,5,1,2 1.0954451150103 35133,5,1,3 0.94868329805051 35143,5,1,4 0.89442719099992 35153,5,1,5 0.86602540378444 35163,5,1,6 0.84852813742386 35173,5,1,7 0.83666002653408 35183,5,1,8 0.82807867121083 35233,5,2,3 1.3416407864999 35243,5,2,4 1.0954451150103 35253,5,2,5 1 35263,5,2,6 0.94868329805051 35273,5,2,7 0.91651513899117 35283,5,2,8 0.89442719099992 35343,5,3,4 1.549193338483 35353,5,3,5 1.2247448713916 35363,5,3,6 1.0954451150103 35373,5,3,7 1.024695076596 35383,5,3,8 0.97979589711327 35453,5,4,5 1.7320508075689 35463,5,4,6 1.3416407864999 35473,5,4,7 1.1832159566199 35483,5,4,8 1.0954451150103 35563,5,5,6 1.897366596101 35573,5,5,7 1.4491376746189 35583,5,5,8 1.2649110640674 35673,5,6,7 2.0493901531919 35683,5,6,8 1.549193338483 35783,5,7,8 2.1908902300207 36123,6,1,2 1 36133,6,1,3 0.86602540378444 36143,6,1,4 0.81649658092773 36153,6,1,5 0.79056941504209 36163,6,1,6 0.77459666924148 36173,6,1,7 0.76376261582597 36183,6,1,8 0.75592894601845 36233,6,2,3 1.2247448713916 36243,6,2,4 1 36253,6,2,5 0.91287092917528 36263,6,2,6 0.86602540378444 36273,6,2,7 0.83666002653408 36283,6,2,8 0.81649658092773 36343,6,3,4 1.4142135623731 36353,6,3,5 1.1180339887499 36363,6,3,6 1 36373,6,3,7 0.93541434669349 36383,6,3,8 0.89442719099992 36453,6,4,5 1.5811388300842 36463,6,4,6 1.2247448713916 36473,6,4,7 1.0801234497346 36483,6,4,8 1 36563,6,5,6 1.7320508075689 36573,6,5,7 1.3228756555323 36583,6,5,8 1.1547005383793 36673,6,6,7 1.870828693387 36683,6,6,8 1.4142135623731 36783,6,7,8 2 37123,7,1,2 0.92582009977255 37133,7,1,3 0.80178372573727 37143,7,1,4 0.75592894601845 37153,7,1,5 0.7319250547114 37163,7,1,6 0.71713716560064 37173,7,1,7 0.70710678118655 37183,7,1,8 0.69985421222377 37233,7,2,3 1.1338934190277 37243,7,2,4 0.92582009977255 37253,7,2,5 0.84515425472852 37263,7,2,6 0.80178372573727 37273,7,2,7 0.77459666924148 37283,7,2,8 0.75592894601845 37343,7,3,4 1.309307341416 37353,7,3,5 1.0350983390135 37363,7,3,6 0.92582009977255 37373,7,3,7 0.86602540378444 37383,7,3,8 0.82807867121083 37453,7,4,5 1.4638501094228 37463,7,4,6 1.1338934190277 37473,7,4,7 1 37483,7,4,8 0.92582009977255 37563,7,5,6 1.6035674514745 37573,7,5,7 1.2247448713916 37583,7,5,8 1.0690449676497 37673,7,6,7 1.7320508075689 37683,7,6,8 1.309307341416 37783,7,7,8 1.8516401995451 38123,8,1,2 0.86602540378444 38133,8,1,3 0.75 38143,8,1,4 0.70710678118655 38153,8,1,5 0.68465319688146 38163,8,1,6 0.67082039324994 38173,8,1,7 0.66143782776615 38183,8,1,8 0.65465367070798 38233,8,2,3 1.0606601717798 38243,8,2,4 0.86602540378444 38253,8,2,5 0.79056941504209 38263,8,2,6 0.75 38273,8,2,7 0.72456883730947 38283,8,2,8 0.70710678118655 38343,8,3,4 1.2247448713916 38353,8,3,5 0.96824583655185 38363,8,3,6 0.86602540378444 38373,8,3,7 0.81009258730098 38383,8,3,8 0.77459666924148 38453,8,4,5 1.3693063937629 38463,8,4,6 1.0606601717798 38473,8,4,7 0.93541434669349 38483,8,4,8 0.86602540378444 38563,8,5,6 1.5 38573,8,5,7 1.145643923739 38583,8,5,8 1 38673,8,6,7 1.620185174602 38683,8,6,8 1.2247448713916 38783,8,7,8 1.7320508075689 41124,1,1,2 2.8284271247462 41134,1,1,3 2.4494897427832 41144,1,1,4 2.3094010767585 41154,1,1,5 2.2360679774998 41164,1,1,6 2.1908902300207 41174,1,1,7 2.1602468994693 41184,1,1,8 2.1380899352994 41234,1,2,3 3.4641016151378 41244,1,2,4 2.8284271247462 41254,1,2,5 2.5819888974716 41264,1,2,6 2.4494897427832 41274,1,2,7 2.3664319132398 41284,1,2,8 2.3094010767585 41344,1,3,4 4 41354,1,3,5 3.1622776601684 41364,1,3,6 2.8284271247462 41374,1,3,7 2.6457513110646 41384,1,3,8 2.5298221281347 41454,1,4,5 4.4721359549996 41464,1,4,6 3.4641016151378 41474,1,4,7 3.0550504633039 41484,1,4,8 2.8284271247462 41564,1,5,6 4.8989794855664 41574,1,5,7 3.7416573867739 41584,1,5,8 3.2659863237109 41674,1,6,7 5.2915026221292 41684,1,6,8 4 41784,1,7,8 5.6568542494924 42124,2,1,2 2 42134,2,1,3 1.7320508075689 42144,2,1,4 1.6329931618555 42154,2,1,5 1.5811388300842 42164,2,1,6 1.549193338483 42174,2,1,7 1.5275252316519 42184,2,1,8 1.5118578920369 42234,2,2,3 2.4494897427832 42244,2,2,4 2 42254,2,2,5 1.8257418583506 42264,2,2,6 1.7320508075689 42274,2,2,7 1.6733200530682 42284,2,2,8 1.6329931618555 42344,2,3,4 2.8284271247462 42354,2,3,5 2.2360679774998 42364,2,3,6 2 42374,2,3,7 1.870828693387 42384,2,3,8 1.7888543819998 42454,2,4,5 3.1622776601684 42464,2,4,6 2.4494897427832 42474,2,4,7 2.1602468994693 42484,2,4,8 2 42564,2,5,6 3.4641016151378 42574,2,5,7 2.6457513110646 42584,2,5,8 2.3094010767585 42674,2,6,7 3.7416573867739 42684,2,6,8 2.8284271247462 42784,2,7,8 4 43124,3,1,2 1.6329931618555 43134,3,1,3 1.4142135623731 43144,3,1,4 1.3333333333333 43154,3,1,5 1.2909944487358 43164,3,1,6 1.2649110640674 43174,3,1,7 1.2472191289246 43184,3,1,8 1.2344267996967 43234,3,2,3 2 43244,3,2,4 1.6329931618555 43254,3,2,5 1.4907119849999 43264,3,2,6 1.4142135623731 43274,3,2,7 1.3662601021279 43284,3,2,8 1.3333333333333 43344,3,3,4 2.3094010767585 43354,3,3,5 1.8257418583506 43364,3,3,6 1.6329931618555 43374,3,3,7 1.5275252316519 43384,3,3,8 1.4605934866804 43454,3,4,5 2.5819888974716 43464,3,4,6 2 43474,3,4,7 1.7638342073764 43484,3,4,8 1.6329931618555 43564,3,5,6 2.8284271247462 43574,3,5,7 2.1602468994693 43584,3,5,8 1.8856180831641 43674,3,6,7 3.0550504633039 43684,3,6,8 2.3094010767585 43784,3,7,8 3.2659863237109 44124,4,1,2 1.4142135623731 44134,4,1,3 1.2247448713916 44144,4,1,4 1.1547005383793 44154,4,1,5 1.1180339887499 44164,4,1,6 1.0954451150103 44174,4,1,7 1.0801234497346 44184,4,1,8 1.0690449676497 44234,4,2,3 1.7320508075689 44244,4,2,4 1.4142135623731 44254,4,2,5 1.2909944487358 44264,4,2,6 1.2247448713916 44274,4,2,7 1.1832159566199 44284,4,2,8 1.1547005383793 44344,4,3,4 2 44354,4,3,5 1.5811388300842 44364,4,3,6 1.4142135623731 44374,4,3,7 1.3228756555323 44384,4,3,8 1.2649110640674 44454,4,4,5 2.2360679774998 44464,4,4,6 1.7320508075689 44474,4,4,7 1.5275252316519 44484,4,4,8 1.4142135623731 44564,4,5,6 2.4494897427832 44574,4,5,7 1.870828693387 44584,4,5,8 1.6329931618555 44674,4,6,7 2.6457513110646 44684,4,6,8 2 44784,4,7,8 2.8284271247462 45124,5,1,2 1.2649110640674 45134,5,1,3 1.0954451150103 45144,5,1,4 1.0327955589886 45154,5,1,5 1 45164,5,1,6 0.97979589711327 45174,5,1,7 0.9660917830793 45184,5,1,8 0.95618288746751 45234,5,2,3 1.549193338483 45244,5,2,4 1.2649110640674 45254,5,2,5 1.1547005383793 45264,5,2,6 1.0954451150103 45274,5,2,7 1.0583005244258 45284,5,2,8 1.0327955589886 45344,5,3,4 1.7888543819998 45354,5,3,5 1.4142135623731 45364,5,3,6 1.2649110640674 45374,5,3,7 1.1832159566199 45384,5,3,8 1.1313708498985 45454,5,4,5 2 45464,5,4,6 1.549193338483 45474,5,4,7 1.3662601021279 45484,5,4,8 1.2649110640674 45564,5,5,6 2.1908902300207 45574,5,5,7 1.6733200530682 45584,5,5,8 1.4605934866804 45674,5,6,7 2.3664319132398 45684,5,6,8 1.7888543819998 45784,5,7,8 2.5298221281347 46124,6,1,2 1.1547005383793 46134,6,1,3 1 46144,6,1,4 0.94280904158206 46154,6,1,5 0.91287092917528 46164,6,1,6 0.89442719099992 46174,6,1,7 0.8819171036882 46184,6,1,8 0.87287156094397 46234,6,2,3 1.4142135623731 46244,6,2,4 1.1547005383793 46254,6,2,5 1.0540925533895 46264,6,2,6 1 46274,6,2,7 0.9660917830793 46284,6,2,8 0.94280904158206 46344,6,3,4 1.6329931618555 46354,6,3,5 1.2909944487358 46364,6,3,6 1.1547005383793 46374,6,3,7 1.0801234497346 46384,6,3,8 1.0327955589886 46454,6,4,5 1.8257418583506 46464,6,4,6 1.4142135623731 46474,6,4,7 1.2472191289246 46484,6,4,8 1.1547005383793 46564,6,5,6 2 46574,6,5,7 1.5275252316519 46584,6,5,8 1.3333333333333 46674,6,6,7 2.1602468994693 46684,6,6,8 1.6329931618555 46784,6,7,8 2.3094010767585 47124,7,1,2 1.0690449676497 47134,7,1,3 0.92582009977255 47144,7,1,4 0.87287156094397 47154,7,1,5 0.84515425472852 47164,7,1,6 0.82807867121083 47174,7,1,7 0.81649658092773 47184,7,1,8 0.80812203564177 47234,7,2,3 1.309307341416 47244,7,2,4 1.0690449676497 47254,7,2,5 0.97590007294853 47264,7,2,6 0.92582009977255 47274,7,2,7 0.89442719099992 47284,7,2,8 0.87287156094397 47344,7,3,4 1.5118578920369 47354,7,3,5 1.1952286093344 47364,7,3,6 1.0690449676497 47374,7,3,7 1 47384,7,3,8 0.95618288746751 47454,7,4,5 1.690308509457 47464,7,4,6 1.309307341416 47474,7,4,7 1.1547005383793 47484,7,4,8 1.0690449676497 47564,7,5,6 1.8516401995451 47574,7,5,7 1.4142135623731 47584,7,5,8 1.2344267996967 47674,7,6,7 2 47684,7,6,8 1.5118578920369 47784,7,7,8 2.1380899352994 48124,8,1,2 1 48134,8,1,3 0.86602540378444 48144,8,1,4 0.81649658092773 48154,8,1,5 0.79056941504209 48164,8,1,6 0.77459666924148 48174,8,1,7 0.76376261582597 48184,8,1,8 0.75592894601845 48234,8,2,3 1.2247448713916 48244,8,2,4 1 48254,8,2,5 0.91287092917528 48264,8,2,6 0.86602540378444 48274,8,2,7 0.83666002653408 48284,8,2,8 0.81649658092773 48344,8,3,4 1.4142135623731 48354,8,3,5 1.1180339887499 48364,8,3,6 1 48374,8,3,7 0.93541434669349 48384,8,3,8 0.89442719099992 48454,8,4,5 1.5811388300842 48464,8,4,6 1.2247448713916 48474,8,4,7 1.0801234497346 48484,8,4,8 1 48564,8,5,6 1.7320508075689 48574,8,5,7 1.3228756555323 48584,8,5,8 1.1547005383793 48674,8,6,7 1.870828693387 48684,8,6,8 1.4142135623731 48784,8,7,8 2 51125,1,1,2 3.1622776601684 51135,1,1,3 2.7386127875258 51145,1,1,4 2.5819888974716 51155,1,1,5 2.5 51165,1,1,6 2.4494897427832 51175,1,1,7 2.4152294576982 51185,1,1,8 2.3904572186688 51235,1,2,3 3.8729833462074 51245,1,2,4 3.1622776601684 51255,1,2,5 2.8867513459481 51265,1,2,6 2.7386127875258 51275,1,2,7 2.6457513110646 51285,1,2,8 2.5819888974716 51345,1,3,4 4.4721359549996 51355,1,3,5 3.5355339059327 51365,1,3,6 3.1622776601684 51375,1,3,7 2.9580398915498 51385,1,3,8 2.8284271247462 51455,1,4,5 5 51465,1,4,6 3.8729833462074 51475,1,4,7 3.4156502553199 51485,1,4,8 3.1622776601684 51565,1,5,6 5.4772255750517 51575,1,5,7 4.1833001326704 51585,1,5,8 3.6514837167011 51675,1,6,7 5.9160797830996 51685,1,6,8 4.4721359549996 51785,1,7,8 6.3245553203368 52125,2,1,2 2.2360679774998 52135,2,1,3 1.9364916731037 52145,2,1,4 1.8257418583506 52155,2,1,5 1.7677669529664 52165,2,1,6 1.7320508075689 52175,2,1,7 1.7078251276599 52185,2,1,8 1.690308509457 52235,2,2,3 2.7386127875258 52245,2,2,4 2.2360679774998 52255,2,2,5 2.0412414523193 52265,2,2,6 1.9364916731037 52275,2,2,7 1.870828693387 52285,2,2,8 1.8257418583506 52345,2,3,4 3.1622776601684 52355,2,3,5 2.5 52365,2,3,6 2.2360679774998 52375,2,3,7 2.0916500663352 52385,2,3,8 2 52455,2,4,5 3.5355339059327 52465,2,4,6 2.7386127875258 52475,2,4,7 2.4152294576982 52485,2,4,8 2.2360679774998 52565,2,5,6 3.8729833462074 52575,2,5,7 2.9580398915498 52585,2,5,8 2.5819888974716 52675,2,6,7 4.1833001326704 52685,2,6,8 3.1622776601684 52785,2,7,8 4.4721359549996 53125,3,1,2 1.8257418583506 53135,3,1,3 1.5811388300842 53145,3,1,4 1.4907119849999 53155,3,1,5 1.4433756729741 53165,3,1,6 1.4142135623731 53175,3,1,7 1.3944333775568 53185,3,1,8 1.3801311186847 53235,3,2,3 2.2360679774998 53245,3,2,4 1.8257418583506 53255,3,2,5 1.6666666666667 53265,3,2,6 1.5811388300842 53275,3,2,7 1.5275252316519 53285,3,2,8 1.4907119849999 53345,3,3,4 2.5819888974716 53355,3,3,5 2.0412414523193 53365,3,3,6 1.8257418583506 53375,3,3,7 1.7078251276599 53385,3,3,8 1.6329931618555 53455,3,4,5 2.8867513459481 53465,3,4,6 2.2360679774998 53475,3,4,7 1.9720265943665 53485,3,4,8 1.8257418583506 53565,3,5,6 3.1622776601684 53575,3,5,7 2.4152294576982 53585,3,5,8 2.1081851067789 53675,3,6,7 3.4156502553199 53685,3,6,8 2.5819888974716 53785,3,7,8 3.6514837167011 54125,4,1,2 1.5811388300842 54135,4,1,3 1.3693063937629 54145,4,1,4 1.2909944487358 54155,4,1,5 1.25 54165,4,1,6 1.2247448713916 54175,4,1,7 1.2076147288491 54185,4,1,8 1.1952286093344 54235,4,2,3 1.9364916731037 54245,4,2,4 1.5811388300842 54255,4,2,5 1.4433756729741 54265,4,2,6 1.3693063937629 54275,4,2,7 1.3228756555323 54285,4,2,8 1.2909944487358 54345,4,3,4 2.2360679774998 54355,4,3,5 1.7677669529664 54365,4,3,6 1.5811388300842 54375,4,3,7 1.4790199457749 54385,4,3,8 1.4142135623731 54455,4,4,5 2.5 54465,4,4,6 1.9364916731037 54475,4,4,7 1.7078251276599 54485,4,4,8 1.5811388300842 54565,4,5,6 2.7386127875258 54575,4,5,7 2.0916500663352 54585,4,5,8 1.8257418583506 54675,4,6,7 2.9580398915498 54685,4,6,8 2.2360679774998 54785,4,7,8 3.1622776601684 55125,5,1,2 1.4142135623731 55135,5,1,3 1.2247448713916 55145,5,1,4 1.1547005383793 55155,5,1,5 1.1180339887499 55165,5,1,6 1.0954451150103 55175,5,1,7 1.0801234497346 55185,5,1,8 1.0690449676497 55235,5,2,3 1.7320508075689 55245,5,2,4 1.4142135623731 55255,5,2,5 1.2909944487358 55265,5,2,6 1.2247448713916 55275,5,2,7 1.1832159566199 55285,5,2,8 1.1547005383793 55345,5,3,4 2 55355,5,3,5 1.5811388300842 55365,5,3,6 1.4142135623731 55375,5,3,7 1.3228756555323 55385,5,3,8 1.2649110640674 55455,5,4,5 2.2360679774998 55465,5,4,6 1.7320508075689 55475,5,4,7 1.5275252316519 55485,5,4,8 1.4142135623731 55565,5,5,6 2.4494897427832 55575,5,5,7 1.870828693387 55585,5,5,8 1.6329931618555 55675,5,6,7 2.6457513110646 55685,5,6,8 2 55785,5,7,8 2.8284271247462 56125,6,1,2 1.2909944487358 56135,6,1,3 1.1180339887499 56145,6,1,4 1.0540925533895 56155,6,1,5 1.0206207261597 56165,6,1,6 1 56175,6,1,7 0.98601329718327 56185,6,1,8 0.97590007294853 56235,6,2,3 1.5811388300842 56245,6,2,4 1.2909944487358 56255,6,2,5 1.1785113019776 56265,6,2,6 1.1180339887499 56275,6,2,7 1.0801234497346 56285,6,2,8 1.0540925533895 56345,6,3,4 1.8257418583506 56355,6,3,5 1.4433756729741 56365,6,3,6 1.2909944487358 56375,6,3,7 1.2076147288491 56385,6,3,8 1.1547005383793 56455,6,4,5 2.0412414523193 56465,6,4,6 1.5811388300842 56475,6,4,7 1.3944333775568 56485,6,4,8 1.2909944487358 56565,6,5,6 2.2360679774998 56575,6,5,7 1.7078251276599 56585,6,5,8 1.4907119849999 56675,6,6,7 2.4152294576982 56685,6,6,8 1.8257418583506 56785,6,7,8 2.5819888974716 57125,7,1,2 1.1952286093344 57135,7,1,3 1.0350983390135 57145,7,1,4 0.97590007294853 57155,7,1,5 0.94491118252307 57165,7,1,6 0.92582009977255 57175,7,1,7 0.91287092917528 57185,7,1,8 0.90350790290525 57235,7,2,3 1.4638501094228 57245,7,2,4 1.1952286093344 57255,7,2,5 1.09108945118 57265,7,2,6 1.0350983390135 57275,7,2,7 1 57285,7,2,8 0.97590007294853 57345,7,3,4 1.690308509457 57355,7,3,5 1.3363062095621 57365,7,3,6 1.1952286093344 57375,7,3,7 1.1180339887499 57385,7,3,8 1.0690449676497 57455,7,4,5 1.8898223650461 57465,7,4,6 1.4638501094228 57475,7,4,7 1.2909944487358 57485,7,4,8 1.1952286093344 57565,7,5,6 2.0701966780271 57575,7,5,7 1.5811388300842 57585,7,5,8 1.3801311186847 57675,7,6,7 2.2360679774998 57685,7,6,8 1.690308509457 57785,7,7,8 2.3904572186688 58125,8,1,2 1.1180339887499 58135,8,1,3 0.96824583655185 58145,8,1,4 0.91287092917528 58155,8,1,5 0.88388347648318 58165,8,1,6 0.86602540378444 58175,8,1,7 0.85391256382997 58185,8,1,8 0.84515425472852 58235,8,2,3 1.3693063937629 58245,8,2,4 1.1180339887499 58255,8,2,5 1.0206207261597 58265,8,2,6 0.96824583655185 58275,8,2,7 0.93541434669349 58285,8,2,8 0.91287092917528 58345,8,3,4 1.5811388300842 58355,8,3,5 1.25 58365,8,3,6 1.1180339887499 58375,8,3,7 1.0458250331676 58385,8,3,8 1 58455,8,4,5 1.7677669529664 58465,8,4,6 1.3693063937629 58475,8,4,7 1.2076147288491 58485,8,4,8 1.1180339887499 58565,8,5,6 1.9364916731037 58575,8,5,7 1.4790199457749 58585,8,5,8 1.2909944487358 58675,8,6,7 2.0916500663352 58685,8,6,8 1.5811388300842 58785,8,7,8 2.2360679774998 61126,1,1,2 3.4641016151378 61136,1,1,3 3 61146,1,1,4 2.8284271247462 61156,1,1,5 2.7386127875258 61166,1,1,6 2.6832815729997 61176,1,1,7 2.6457513110646 61186,1,1,8 2.6186146828319 61236,1,2,3 4.2426406871193 61246,1,2,4 3.4641016151378 61256,1,2,5 3.1622776601684 61266,1,2,6 3 61276,1,2,7 2.8982753492379 61286,1,2,8 2.8284271247462 61346,1,3,4 4.8989794855664 61356,1,3,5 3.8729833462074 61366,1,3,6 3.4641016151378 61376,1,3,7 3.2403703492039 61386,1,3,8 3.0983866769659 61456,1,4,5 5.4772255750517 61466,1,4,6 4.2426406871193 61476,1,4,7 3.7416573867739 61486,1,4,8 3.4641016151378 61566,1,5,6 6 61576,1,5,7 4.5825756949558 61586,1,5,8 4 61676,1,6,7 6.4807406984079 61686,1,6,8 4.8989794855664 61786,1,7,8 6.9282032302755 62126,2,1,2 2.4494897427832 62136,2,1,3 2.1213203435596 62146,2,1,4 2 62156,2,1,5 1.9364916731037 62166,2,1,6 1.897366596101 62176,2,1,7 1.870828693387 62186,2,1,8 1.8516401995451 62236,2,2,3 3 62246,2,2,4 2.4494897427832 62256,2,2,5 2.2360679774998 62266,2,2,6 2.1213203435596 62276,2,2,7 2.0493901531919 62286,2,2,8 2 62346,2,3,4 3.4641016151378 62356,2,3,5 2.7386127875258 62366,2,3,6 2.4494897427832 62376,2,3,7 2.2912878474779 62386,2,3,8 2.1908902300207 62456,2,4,5 3.8729833462074 62466,2,4,6 3 62476,2,4,7 2.6457513110646 62486,2,4,8 2.4494897427832 62566,2,5,6 4.2426406871193 62576,2,5,7 3.2403703492039 62586,2,5,8 2.8284271247462 62676,2,6,7 4.5825756949558 62686,2,6,8 3.4641016151378 62786,2,7,8 4.8989794855664 63126,3,1,2 2 63136,3,1,3 1.7320508075689 63146,3,1,4 1.6329931618555 63156,3,1,5 1.5811388300842 63166,3,1,6 1.549193338483 63176,3,1,7 1.5275252316519 63186,3,1,8 1.5118578920369 63236,3,2,3 2.4494897427832 63246,3,2,4 2 63256,3,2,5 1.8257418583506 63266,3,2,6 1.7320508075689 63276,3,2,7 1.6733200530682 63286,3,2,8 1.6329931618555 63346,3,3,4 2.8284271247462 63356,3,3,5 2.2360679774998 63366,3,3,6 2 63376,3,3,7 1.870828693387 63386,3,3,8 1.7888543819998 63456,3,4,5 3.1622776601684 63466,3,4,6 2.4494897427832 63476,3,4,7 2.1602468994693 63486,3,4,8 2 63566,3,5,6 3.4641016151378 63576,3,5,7 2.6457513110646 63586,3,5,8 2.3094010767585 63676,3,6,7 3.7416573867739 63686,3,6,8 2.8284271247462 63786,3,7,8 4 64126,4,1,2 1.7320508075689 64136,4,1,3 1.5 64146,4,1,4 1.4142135623731 64156,4,1,5 1.3693063937629 64166,4,1,6 1.3416407864999 64176,4,1,7 1.3228756555323 64186,4,1,8 1.309307341416 64236,4,2,3 2.1213203435596 64246,4,2,4 1.7320508075689 64256,4,2,5 1.5811388300842 64266,4,2,6 1.5 64276,4,2,7 1.4491376746189 64286,4,2,8 1.4142135623731 64346,4,3,4 2.4494897427832 64356,4,3,5 1.9364916731037 64366,4,3,6 1.7320508075689 64376,4,3,7 1.620185174602 64386,4,3,8 1.549193338483 64456,4,4,5 2.7386127875258 64466,4,4,6 2.1213203435596 64476,4,4,7 1.870828693387 64486,4,4,8 1.7320508075689 64566,4,5,6 3 64576,4,5,7 2.2912878474779 64586,4,5,8 2 64676,4,6,7 3.2403703492039 64686,4,6,8 2.4494897427832 64786,4,7,8 3.4641016151378 65126,5,1,2 1.549193338483 65136,5,1,3 1.3416407864999 65146,5,1,4 1.2649110640674 65156,5,1,5 1.2247448713916 65166,5,1,6 1.2 65176,5,1,7 1.1832159566199 65186,5,1,8 1.1710800875382 65236,5,2,3 1.897366596101 65246,5,2,4 1.549193338483 65256,5,2,5 1.4142135623731 65266,5,2,6 1.3416407864999 65276,5,2,7 1.2961481396816 65286,5,2,8 1.2649110640674 65346,5,3,4 2.1908902300207 65356,5,3,5 1.7320508075689 65366,5,3,6 1.549193338483 65376,5,3,7 1.4491376746189 65386,5,3,8 1.3856406460551 65456,5,4,5 2.4494897427832 65466,5,4,6 1.897366596101 65476,5,4,7 1.6733200530682 65486,5,4,8 1.549193338483 65566,5,5,6 2.6832815729997 65576,5,5,7 2.0493901531919 65586,5,5,8 1.7888543819998 65676,5,6,7 2.8982753492379 65686,5,6,8 2.1908902300207 65786,5,7,8 3.0983866769659 66126,6,1,2 1.4142135623731 66136,6,1,3 1.2247448713916 66146,6,1,4 1.1547005383793 66156,6,1,5 1.1180339887499 66166,6,1,6 1.0954451150103 66176,6,1,7 1.0801234497346 66186,6,1,8 1.0690449676497 66236,6,2,3 1.7320508075689 66246,6,2,4 1.4142135623731 66256,6,2,5 1.2909944487358 66266,6,2,6 1.2247448713916 66276,6,2,7 1.1832159566199 66286,6,2,8 1.1547005383793 66346,6,3,4 2 66356,6,3,5 1.5811388300842 66366,6,3,6 1.4142135623731 66376,6,3,7 1.3228756555323 66386,6,3,8 1.2649110640674 66456,6,4,5 2.2360679774998 66466,6,4,6 1.7320508075689 66476,6,4,7 1.5275252316519 66486,6,4,8 1.4142135623731 66566,6,5,6 2.4494897427832 66576,6,5,7 1.870828693387 66586,6,5,8 1.6329931618555 66676,6,6,7 2.6457513110646 66686,6,6,8 2 66786,6,7,8 2.8284271247462 67126,7,1,2 1.309307341416 67136,7,1,3 1.1338934190277 67146,7,1,4 1.0690449676497 67156,7,1,5 1.0350983390135 67166,7,1,6 1.0141851056742 67176,7,1,7 1 67186,7,1,8 0.98974331861079 67236,7,2,3 1.6035674514745 67246,7,2,4 1.309307341416 67256,7,2,5 1.1952286093344 67266,7,2,6 1.1338934190277 67276,7,2,7 1.0954451150103 67286,7,2,8 1.0690449676497 67346,7,3,4 1.8516401995451 67356,7,3,5 1.4638501094228 67366,7,3,6 1.309307341416 67376,7,3,7 1.2247448713916 67386,7,3,8 1.1710800875382 67456,7,4,5 2.0701966780271 67466,7,4,6 1.6035674514745 67476,7,4,7 1.4142135623731 67486,7,4,8 1.309307341416 67566,7,5,6 2.2677868380554 67576,7,5,7 1.7320508075689 67586,7,5,8 1.5118578920369 67676,7,6,7 2.4494897427832 67686,7,6,8 1.8516401995451 67786,7,7,8 2.6186146828319 68126,8,1,2 1.2247448713916 68136,8,1,3 1.0606601717798 68146,8,1,4 1 68156,8,1,5 0.96824583655185 68166,8,1,6 0.94868329805051 68176,8,1,7 0.93541434669349 68186,8,1,8 0.92582009977255 68236,8,2,3 1.5 68246,8,2,4 1.2247448713916 68256,8,2,5 1.1180339887499 68266,8,2,6 1.0606601717798 68276,8,2,7 1.024695076596 68286,8,2,8 1 68346,8,3,4 1.7320508075689 68356,8,3,5 1.3693063937629 68366,8,3,6 1.2247448713916 68376,8,3,7 1.145643923739 68386,8,3,8 1.0954451150103 68456,8,4,5 1.9364916731037 68466,8,4,6 1.5 68476,8,4,7 1.3228756555323 68486,8,4,8 1.2247448713916 68566,8,5,6 2.1213203435596 68576,8,5,7 1.620185174602 68586,8,5,8 1.4142135623731 68676,8,6,7 2.2912878474779 68686,8,6,8 1.7320508075689 68786,8,7,8 2.4494897427832 71127,1,1,2 3.7416573867739 71137,1,1,3 3.2403703492039 71147,1,1,4 3.0550504633039 71157,1,1,5 2.9580398915498 71167,1,1,6 2.8982753492379 71177,1,1,7 2.857738033247 71187,1,1,8 2.8284271247462 71237,1,2,3 4.5825756949558 71247,1,2,4 3.7416573867739 71257,1,2,5 3.4156502553199 71267,1,2,6 3.2403703492039 71277,1,2,7 3.1304951684997 71287,1,2,8 3.0550504633039 71347,1,3,4 5.2915026221292 71357,1,3,5 4.1833001326704 71367,1,3,6 3.7416573867739 71377,1,3,7 3.5 71387,1,3,8 3.3466401061363 71457,1,4,5 5.9160797830996 71467,1,4,6 4.5825756949558 71477,1,4,7 4.0414518843274 71487,1,4,8 3.7416573867739 71567,1,5,6 6.4807406984079 71577,1,5,7 4.9497474683058 71587,1,5,8 4.3204937989386 71677,1,6,7 7 71687,1,6,8 5.2915026221292 71787,1,7,8 7.4833147735479 72127,2,1,2 2.6457513110646 72137,2,1,3 2.2912878474779 72147,2,1,4 2.1602468994693 72157,2,1,5 2.0916500663352 72167,2,1,6 2.0493901531919 72177,2,1,7 2.0207259421637 72187,2,1,8 2 72237,2,2,3 3.2403703492039 72247,2,2,4 2.6457513110646 72257,2,2,5 2.4152294576982 72267,2,2,6 2.2912878474779 72277,2,2,7 2.2135943621179 72287,2,2,8 2.1602468994693 72347,2,3,4 3.7416573867739 72357,2,3,5 2.9580398915498 72367,2,3,6 2.6457513110646 72377,2,3,7 2.4748737341529 72387,2,3,8 2.3664319132398 72457,2,4,5 4.1833001326704 72467,2,4,6 3.2403703492039 72477,2,4,7 2.857738033247 72487,2,4,8 2.6457513110646 72567,2,5,6 4.5825756949558 72577,2,5,7 3.5 72587,2,5,8 3.0550504633039 72677,2,6,7 4.9497474683058 72687,2,6,8 3.7416573867739 72787,2,7,8 5.2915026221292 73127,3,1,2 2.1602468994693 73137,3,1,3 1.870828693387 73147,3,1,4 1.7638342073764 73157,3,1,5 1.7078251276599 73167,3,1,6 1.6733200530682 73177,3,1,7 1.6499158227686 73187,3,1,8 1.6329931618555 73237,3,2,3 2.6457513110646 73247,3,2,4 2.1602468994693 73257,3,2,5 1.9720265943665 73267,3,2,6 1.870828693387 73277,3,2,7 1.8073922282301 73287,3,2,8 1.7638342073764 73347,3,3,4 3.0550504633039 73357,3,3,5 2.4152294576982 73367,3,3,6 2.1602468994693 73377,3,3,7 2.0207259421637 73387,3,3,8 1.9321835661586 73457,3,4,5 3.4156502553199 73467,3,4,6 2.6457513110646 73477,3,4,7 2.3333333333333 73487,3,4,8 2.1602468994693 73567,3,5,6 3.7416573867739 73577,3,5,7 2.857738033247 73587,3,5,8 2.4944382578493 73677,3,6,7 4.0414518843274 73687,3,6,8 3.0550504633039 73787,3,7,8 4.3204937989386 74127,4,1,2 1.870828693387 74137,4,1,3 1.620185174602 74147,4,1,4 1.5275252316519 74157,4,1,5 1.4790199457749 74167,4,1,6 1.4491376746189 74177,4,1,7 1.4288690166235 74187,4,1,8 1.4142135623731 74237,4,2,3 2.2912878474779 74247,4,2,4 1.870828693387 74257,4,2,5 1.7078251276599 74267,4,2,6 1.620185174602 74277,4,2,7 1.5652475842499 74287,4,2,8 1.5275252316519 74347,4,3,4 2.6457513110646 74357,4,3,5 2.0916500663352 74367,4,3,6 1.870828693387 74377,4,3,7 1.75 74387,4,3,8 1.6733200530682 74457,4,4,5 2.9580398915498 74467,4,4,6 2.2912878474779 74477,4,4,7 2.0207259421637 74487,4,4,8 1.870828693387 74567,4,5,6 3.2403703492039 74577,4,5,7 2.4748737341529 74587,4,5,8 2.1602468994693 74677,4,6,7 3.5 74687,4,6,8 2.6457513110646 74787,4,7,8 3.7416573867739 75127,5,1,2 1.6733200530682 75137,5,1,3 1.4491376746189 75147,5,1,4 1.3662601021279 75157,5,1,5 1.3228756555323 75167,5,1,6 1.2961481396816 75177,5,1,7 1.2780193008454 75187,5,1,8 1.2649110640674 75237,5,2,3 2.0493901531919 75247,5,2,4 1.6733200530682 75257,5,2,5 1.5275252316519 75267,5,2,6 1.4491376746189 75277,5,2,7 1.4 75287,5,2,8 1.3662601021279 75347,5,3,4 2.3664319132398 75357,5,3,5 1.870828693387 75367,5,3,6 1.6733200530682 75377,5,3,7 1.5652475842499 75387,5,3,8 1.4966629547096 75457,5,4,5 2.6457513110646 75467,5,4,6 2.0493901531919 75477,5,4,7 1.8073922282301 75487,5,4,8 1.6733200530682 75567,5,5,6 2.8982753492379 75577,5,5,7 2.2135943621179 75587,5,5,8 1.9321835661586 75677,5,6,7 3.1304951684997 75687,5,6,8 2.3664319132398 75787,5,7,8 3.3466401061363 76127,6,1,2 1.5275252316519 76137,6,1,3 1.3228756555323 76147,6,1,4 1.2472191289246 76157,6,1,5 1.2076147288491 76167,6,1,6 1.1832159566199 76177,6,1,7 1.1666666666667 76187,6,1,8 1.1547005383793 76237,6,2,3 1.870828693387 76247,6,2,4 1.5275252316519 76257,6,2,5 1.3944333775568 76267,6,2,6 1.3228756555323 76277,6,2,7 1.2780193008454 76287,6,2,8 1.2472191289246 76347,6,3,4 2.1602468994693 76357,6,3,5 1.7078251276599 76367,6,3,6 1.5275252316519 76377,6,3,7 1.4288690166235 76387,6,3,8 1.3662601021279 76457,6,4,5 2.4152294576982 76467,6,4,6 1.870828693387 76477,6,4,7 1.6499158227686 76487,6,4,8 1.5275252316519 76567,6,5,6 2.6457513110646 76577,6,5,7 2.0207259421637 76587,6,5,8 1.7638342073764 76677,6,6,7 2.857738033247 76687,6,6,8 2.1602468994693 76787,6,7,8 3.0550504633039 77127,7,1,2 1.4142135623731 77137,7,1,3 1.2247448713916 77147,7,1,4 1.1547005383793 77157,7,1,5 1.1180339887499 77167,7,1,6 1.0954451150103 77177,7,1,7 1.0801234497346 77187,7,1,8 1.0690449676497 77237,7,2,3 1.7320508075689 77247,7,2,4 1.4142135623731 77257,7,2,5 1.2909944487358 77267,7,2,6 1.2247448713916 77277,7,2,7 1.1832159566199 77287,7,2,8 1.1547005383793 77347,7,3,4 2 77357,7,3,5 1.5811388300842 77367,7,3,6 1.4142135623731 77377,7,3,7 1.3228756555323 77387,7,3,8 1.2649110640674 77457,7,4,5 2.2360679774998 77467,7,4,6 1.7320508075689 77477,7,4,7 1.5275252316519 77487,7,4,8 1.4142135623731 77567,7,5,6 2.4494897427832 77577,7,5,7 1.870828693387 77587,7,5,8 1.6329931618555 77677,7,6,7 2.6457513110646 77687,7,6,8 2 77787,7,7,8 2.8284271247462 78127,8,1,2 1.3228756555323 78137,8,1,3 1.145643923739 78147,8,1,4 1.0801234497346 78157,8,1,5 1.0458250331676 78167,8,1,6 1.024695076596 78177,8,1,7 1.0103629710818 78187,8,1,8 1 78237,8,2,3 1.620185174602 78247,8,2,4 1.3228756555323 78257,8,2,5 1.2076147288491 78267,8,2,6 1.145643923739 78277,8,2,7 1.1067971810589 78287,8,2,8 1.0801234497346 78347,8,3,4 1.870828693387 78357,8,3,5 1.4790199457749 78367,8,3,6 1.3228756555323 78377,8,3,7 1.2374368670765 78387,8,3,8 1.1832159566199 78457,8,4,5 2.0916500663352 78467,8,4,6 1.620185174602 78477,8,4,7 1.4288690166235 78487,8,4,8 1.3228756555323 78567,8,5,6 2.2912878474779 78577,8,5,7 1.75 78587,8,5,8 1.5275252316519 78677,8,6,7 2.4748737341529 78687,8,6,8 1.870828693387 78787,8,7,8 2.6457513110646 81128,1,1,2 4 81138,1,1,3 3.4641016151378 81148,1,1,4 3.2659863237109 81158,1,1,5 3.1622776601684 81168,1,1,6 3.0983866769659 81178,1,1,7 3.0550504633039 81188,1,1,8 3.0237157840738 81238,1,2,3 4.8989794855664 81248,1,2,4 4 81258,1,2,5 3.6514837167011 81268,1,2,6 3.4641016151378 81278,1,2,7 3.3466401061363 81288,1,2,8 3.2659863237109 81348,1,3,4 5.6568542494924 81358,1,3,5 4.4721359549996 81368,1,3,6 4 81378,1,3,7 3.7416573867739 81388,1,3,8 3.5777087639997 81458,1,4,5 6.3245553203368 81468,1,4,6 4.8989794855664 81478,1,4,7 4.3204937989386 81488,1,4,8 4 81568,1,5,6 6.9282032302755 81578,1,5,7 5.2915026221292 81588,1,5,8 4.618802153517 81678,1,6,7 7.4833147735479 81688,1,6,8 5.6568542494924 81788,1,7,8 8 82128,2,1,2 2.8284271247462 82138,2,1,3 2.4494897427832 82148,2,1,4 2.3094010767585 82158,2,1,5 2.2360679774998 82168,2,1,6 2.1908902300207 82178,2,1,7 2.1602468994693 82188,2,1,8 2.1380899352994 82238,2,2,3 3.4641016151378 82248,2,2,4 2.8284271247462 82258,2,2,5 2.5819888974716 82268,2,2,6 2.4494897427832 82278,2,2,7 2.3664319132398 82288,2,2,8 2.3094010767585 82348,2,3,4 4 82358,2,3,5 3.1622776601684 82368,2,3,6 2.8284271247462 82378,2,3,7 2.6457513110646 82388,2,3,8 2.5298221281347 82458,2,4,5 4.4721359549996 82468,2,4,6 3.4641016151378 82478,2,4,7 3.0550504633039 82488,2,4,8 2.8284271247462 82568,2,5,6 4.8989794855664 82578,2,5,7 3.7416573867739 82588,2,5,8 3.2659863237109 82678,2,6,7 5.2915026221292 82688,2,6,8 4 82788,2,7,8 5.6568542494924 83128,3,1,2 2.3094010767585 83138,3,1,3 2 83148,3,1,4 1.8856180831641 83158,3,1,5 1.8257418583506 83168,3,1,6 1.7888543819998 83178,3,1,7 1.7638342073764 83188,3,1,8 1.7457431218879 83238,3,2,3 2.8284271247462 83248,3,2,4 2.3094010767585 83258,3,2,5 2.1081851067789 83268,3,2,6 2 83278,3,2,7 1.9321835661586 83288,3,2,8 1.8856180831641 83348,3,3,4 3.2659863237109 83358,3,3,5 2.5819888974716 83368,3,3,6 2.3094010767585 83378,3,3,7 2.1602468994693 83388,3,3,8 2.0655911179773 83458,3,4,5 3.6514837167011 83468,3,4,6 2.8284271247462 83478,3,4,7 2.4944382578493 83488,3,4,8 2.3094010767585 83568,3,5,6 4 83578,3,5,7 3.0550504633039 83588,3,5,8 2.6666666666667 83678,3,6,7 4.3204937989386 83688,3,6,8 3.2659863237109 83788,3,7,8 4.618802153517 84128,4,1,2 2 84138,4,1,3 1.7320508075689 84148,4,1,4 1.6329931618555 84158,4,1,5 1.5811388300842 84168,4,1,6 1.549193338483 84178,4,1,7 1.5275252316519 84188,4,1,8 1.5118578920369 84238,4,2,3 2.4494897427832 84248,4,2,4 2 84258,4,2,5 1.8257418583506 84268,4,2,6 1.7320508075689 84278,4,2,7 1.6733200530682 84288,4,2,8 1.6329931618555 84348,4,3,4 2.8284271247462 84358,4,3,5 2.2360679774998 84368,4,3,6 2 84378,4,3,7 1.870828693387 84388,4,3,8 1.7888543819998 84458,4,4,5 3.1622776601684 84468,4,4,6 2.4494897427832 84478,4,4,7 2.1602468994693 84488,4,4,8 2 84568,4,5,6 3.4641016151378 84578,4,5,7 2.6457513110646 84588,4,5,8 2.3094010767585 84678,4,6,7 3.7416573867739 84688,4,6,8 2.8284271247462 84788,4,7,8 4 85128,5,1,2 1.7888543819998 85138,5,1,3 1.549193338483 85148,5,1,4 1.4605934866804 85158,5,1,5 1.4142135623731 85168,5,1,6 1.3856406460551 85178,5,1,7 1.3662601021279 85188,5,1,8 1.3522468075656 85238,5,2,3 2.1908902300207 85248,5,2,4 1.7888543819998 85258,5,2,5 1.6329931618555 85268,5,2,6 1.549193338483 85278,5,2,7 1.4966629547096 85288,5,2,8 1.4605934866804 85348,5,3,4 2.5298221281347 85358,5,3,5 2 85368,5,3,6 1.7888543819998 85378,5,3,7 1.6733200530682 85388,5,3,8 1.6 85458,5,4,5 2.8284271247462 85468,5,4,6 2.1908902300207 85478,5,4,7 1.9321835661586 85488,5,4,8 1.7888543819998 85568,5,5,6 3.0983866769659 85578,5,5,7 2.3664319132398 85588,5,5,8 2.0655911179773 85678,5,6,7 3.3466401061363 85688,5,6,8 2.5298221281347 85788,5,7,8 3.5777087639997 86128,6,1,2 1.6329931618555 86138,6,1,3 1.4142135623731 86148,6,1,4 1.3333333333333 86158,6,1,5 1.2909944487358 86168,6,1,6 1.2649110640674 86178,6,1,7 1.2472191289246 86188,6,1,8 1.2344267996967 86238,6,2,3 2 86248,6,2,4 1.6329931618555 86258,6,2,5 1.4907119849999 86268,6,2,6 1.4142135623731 86278,6,2,7 1.3662601021279 86288,6,2,8 1.3333333333333 86348,6,3,4 2.3094010767585 86358,6,3,5 1.8257418583506 86368,6,3,6 1.6329931618555 86378,6,3,7 1.5275252316519 86388,6,3,8 1.4605934866804 86458,6,4,5 2.5819888974716 86468,6,4,6 2 86478,6,4,7 1.7638342073764 86488,6,4,8 1.6329931618555 86568,6,5,6 2.8284271247462 86578,6,5,7 2.1602468994693 86588,6,5,8 1.8856180831641 86678,6,6,7 3.0550504633039 86688,6,6,8 2.3094010767585 86788,6,7,8 3.2659863237109 87128,7,1,2 1.5118578920369 87138,7,1,3 1.309307341416 87148,7,1,4 1.2344267996967 87158,7,1,5 1.1952286093344 87168,7,1,6 1.1710800875382 87178,7,1,7 1.1547005383793 87188,7,1,8 1.1428571428571 87238,7,2,3 1.8516401995451 87248,7,2,4 1.5118578920369 87258,7,2,5 1.3801311186847 87268,7,2,6 1.309307341416 87278,7,2,7 1.2649110640674 87288,7,2,8 1.2344267996967 87348,7,3,4 2.1380899352994 87358,7,3,5 1.690308509457 87368,7,3,6 1.5118578920369 87378,7,3,7 1.4142135623731 87388,7,3,8 1.3522468075656 87458,7,4,5 2.3904572186688 87468,7,4,6 1.8516401995451 87478,7,4,7 1.6329931618555 87488,7,4,8 1.5118578920369 87568,7,5,6 2.6186146828319 87578,7,5,7 2 87588,7,5,8 1.7457431218879 87678,7,6,7 2.8284271247462 87688,7,6,8 2.1380899352994 87788,7,7,8 3.0237157840738 88128,8,1,2 1.4142135623731 88138,8,1,3 1.2247448713916 88148,8,1,4 1.1547005383793 88158,8,1,5 1.1180339887499 88168,8,1,6 1.0954451150103 88178,8,1,7 1.0801234497346 88188,8,1,8 1.0690449676497 88238,8,2,3 1.7320508075689 88248,8,2,4 1.4142135623731 88258,8,2,5 1.2909944487358 88268,8,2,6 1.2247448713916 88278,8,2,7 1.1832159566199 88288,8,2,8 1.1547005383793 88348,8,3,4 2 88358,8,3,5 1.5811388300842 88368,8,3,6 1.4142135623731 88378,8,3,7 1.3228756555323 88388,8,3,8 1.2649110640674 88458,8,4,5 2.2360679774998 88468,8,4,6 1.7320508075689 88478,8,4,7 1.5275252316519 88488,8,4,8 1.4142135623731 88568,8,5,6 2.4494897427832 88578,8,5,7 1.870828693387 88588,8,5,8 1.6329931618555 88678,8,6,7 2.6457513110646 88688,8,6,8 2 88788,8,7,8 2.8284271247462There are many ways in which irrep-tile parallograms can be constructed.
The simplest to take a rep-tile, and dissect one or more of the copies further, as in the examples of the square, √2:1 rectangle, √3:1 rectangle and domino below.
| 1,2,2,4 1 | 1,1,1,2 1.4142135623731 | 1,1,2,4 1.4142135623731 | |
| 1,1,2,3 1.7320508075689 | 1,1,2,3 1.7320508075689 | 2,1,1,3 1.7320508075689 | 2,1,1,3 1.7320508075689 |
| 3,1,1,4 2 | 2,1,2,4 2 |
A greater variety can be generated from the rep-n2 parallelograms (n > 2). A block of k2 (k<n) parallelograms can be replaced by a single parallelogram. This can be repeated while blocks of m2 parallelograms (m≥2) remain. A similar process can be applied to the rep-mn parallelograms.
| n=3 |
| n=5 | ||||
| n=5 | ||||
| n=5 |
The metallic means are numbers of the form (n + √(n2+4))/2. They are quadratic Pisot numbers, being solutions of the equation x2 - mx - 1 = 0. The relevant Perron numbers are quartic Perron numbers of the form ±i√μ, where μ is a metallic mean. In self-similar tiles associated with those Perron numbers the ratio of the tile to its elements is a integer power of the metallic mean.
The first metallic mean is the golden mean (1+√5)/2. This is associated with the golden rectangle, which has dissection equation c + c3 + c4 = 1.
golden rectangle
If the lower edge is placed with corners at (0,0) and (1,0), and the Perron number is a, then the IFS is { p → ap - a2 + a4; p → ap3 - a3 + a5; p → a4p }.
The second metallic mean is the silver mean (2+√8)/2. This is associated with the silver rectangle, which has dissection equation 2c + 2c3 + c4 = 1. In this case there are 4 alternative dissections.
If the lower edge is placed with corners at (0,0) and (1,0), and the Perron number is a, then the IFS is { p → ap - a2 + a4; p → ap - 2a2 + a4; p → ap3 - a3 + a5; p → ap3 - 2a3 + a5; p → a4p }.
This construction can be generalised for the bronze rectangle and subsequent metallic rectangles. The generalised dissection equation is nc + nc3 + c4 = 1.
The bronze rectangle again has 4 alternative dissections.
Obviously the number of possible dissections increases. For the 4th and 5th metalic rectangles it is 9, and for the 6th and 7th it is 16.
...
Sources:
References
© 2007, 2009, 2014, 2018 Stewart R. Hinsley