Some tiles associated with the 6th unit cubic Pisot number

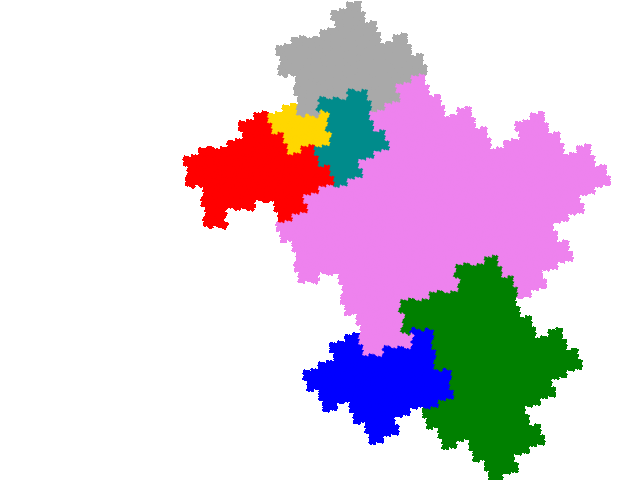
Allodemisymmetric Tiles

As each order 3 tile has 9 potential legitimate order 7 partial post(allo)composition derivatives and there are two order 3 demisymmetric tiles there are a potential 18 order 7 allodemisymmetric tiles. However 7 of the attractors are disconnected, reducing the number to 11.

For the first “external” tile there are 6 derived tiles. Two are simple teragons with dissection equation c + c2 + 3c3 + c4 + c5 = 1 and tiling signature 001122 (demisymmetric tiles have two copies, tiling a symmetric tile, in the unit cell).

allodemisymmetric tileallodemisymmetric tile unit cell

allodemisymmetric tileallodemisymmetric tile unit cell

The other four are complex teragons, two with dissection equation c + c2 + 3c3 + c4 + c5 = 1 and tiling signature 001122,

allodemisymmetric tileallodemisymmetric tile unit cell

allodemisymmetric tile allodemisymmetric tile unit cell

and two with dissection equation c + 2c2 + c3 + 2c5 + c7 = 1 and tiling signature 001144.

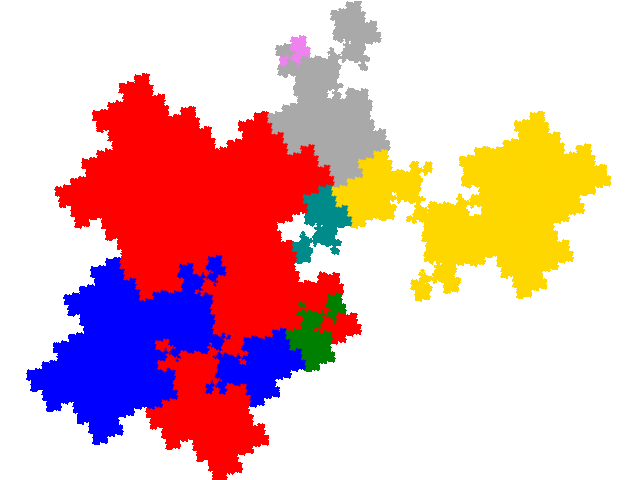
allodemisymmetric tileallodemisymmetric tile unit cell

allodemisymmetric tile allodemisymmetric tile unit cell

The other demisymmetric tile gives rise to 5 derived tiles. They are all complex teragons.

There are three with with dissection equation c + c2 + 3c3 + c4 + c5 = 1 and tiling signature 001122

allodemisymmetric tileallodemisymmetric tile unit cellallodemisymmetric tileallodemisymmetric tile unit cellallodemisymmetric tileallodemisymmetric tile unit cell

and two with dissection equation c + 2c2 + c3 + 2c5 + c7 = 1 and tiling signature 001144.

allodemisymmetric tileallodemisymmetric tile unit cellallodemisymmetric tileallodemisymmetric tile unit cell

© 2017 Stewart R. Hinsley