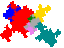
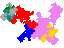
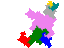
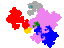
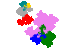
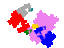
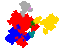
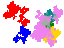
Some tiles associated with the 6th unit
cubic Pisot number
Overview
In 2002 I investigated low order metallic (where the ratio of areas is a
metallic mean) and cubic (where the ratio of areas is a cubic Pisot number)
tiles, including those associated the 6th unit cubic Pisot number (the real
root of x3-2x2-1=0, with a value of approximately
2.20556943040059).
The contraction ratio for such tiles is an integral power of the square root
of the reciprocal of the Pisot number (approximately 0.67334809089831373) and
the rotation the corresponding multiple of approximately
81.2196317797693513°.
- In 2002 I identified 4 order 3 tiles (one with 2 alternative dissections)
and 3 simple order 5 derivatives of one of those tiles.
- Revisiting this in 2015 I identified 2 additional order 3 tiles (and 4
simple order 5 derivatives), and a considerable number of easily generated
order 5 and order 7 derivatives of the original tiles that I didn't get
round to generating in 2002.
- Subsequent investigation in 2016 found two more order 3 tiles, with 6
order 5 and 4 order 7 derivatives
- In 2017 I added a further order 5 tile, and 54 futher order 7 derivatives
(partial postallocomposition derivatives) of the order 3 tiles
This gives a total of 694 tiles (8 order 3
tiles, 60 order 5 tiles and 626 order 7 tiles). There may well be other tiles.
There are predicted to be several thousand order 9 tiles.
The tiles are (click on a tile for a larger image and more details)
From 2002






From 2015


Derivatives added 2015
Order 5 fractional (unitary) tiles (grouped element tiles)














Order 5 fractional (non-unitary) tiles (partial postcomposition tiles)








Order 7 fractional (unitary) tiles (grouped element tiles)
















































































































































Order 7 fractional (non-unitary) tiles (partial postcomposition tiles)











More new discoveries from 2015
More order 5 fractional (non-unitary) tiles
















More order 7 fractional (non-unitary) tiles











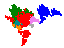

























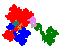






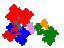
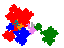































From 2016








From 2017















































© 2015, 2016, 2017 Stewart R. Hinsley



