

In the case of allosymmetric tiles (partial postallocomposition derivatives of the symmetric tile) it is useful to distinguish between legitimate (combinations of a form that reliably produces tiles, i.e. using the same IFS for the symmetric tile) and illegitimate (combinations using different IFSs for the symmetric tile that “just happen” to work) IFSs and with the former group between fertile (giving access to additional tiles via the co-cell technique) and sterile (not giving access to additional tiles via the co-cell technique).
The symmetric tile is 8-fold degenerate. However half of the of the derived tiles are equivalent to the other half rotated by 180°. Therefore, as an order 3 tile has 9 potential partial postallocomposition derivatives this means that there are 18 potential legitimate and fertile, and 18 potential legitimate and sterile, IFSs.
Of the 18 legitimate and fertile IFS 4 are disconnected, and 6 of the remainder come in pairs with the same attractor but different dissections (a block of 3 elements can be rotated by 180°) reducing the number of tiles to 11.
There is a simple teragon with dissection equation c+c2+3c3+c4+c5. This has three copies in the unit cell, with signature 012. The cell transforms are { p → p; p →ap + 1 + a; p →a2p + 1 - a2 }. (It is 4-fold pseudo-degenerate, with two of the dissections fertile and two sterile.)


There are two complex teragons with the same dissection equation and signature.




There are four more visually somewhat similar complex teragons with dissection equation c+2c2+c3+2c5+c7 and signature 014.








4 are visually close to the windowed tile - they can be viewed as being windowed tiles with two small copies partially filling each of the windows. These have dissection equation 2c+c4+2c5+c6+c7.




Three copies, with signature 034, make up a symmetric tile, and hence also a unit cell. The cell transforms are { p → p; p →±a3p; p →±a4p - 1 }. (The signs applicable depend on which of the degenerate versions of the symmetric tile is used as a base.)




There are the same potential number of legitimate but sterile (not giving access to other tiles via the co-cell technique). The attractors include alternate dissections of the simple teragon and the last 4 tiles above. Once this, and other eliminations, are taken into account there are an additional two complex teragons similar to the two above, and 4 more complex teragons similar to the order 7 metasymmetric tiles, but in this case not identical to them. Thus we have a total of 17 legitimate allosymmetric tiles.
The pair of complex teragons, as above, have dissection equation c+c2+3c3+c4+c5.


They have three copies in the unit cell, with signature 012.


The remaining 4 tiles have dissection equation c+2c2+c3+2c5+c7.


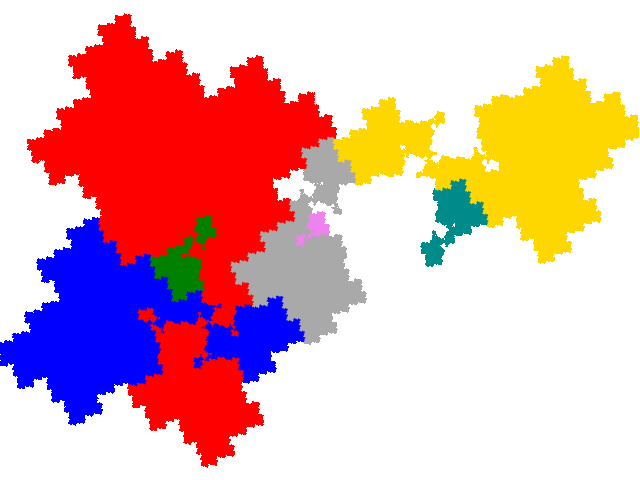

They have three copies in the unit cell, with signature 014.




© 2017 Stewart R. Hinsley