

In addition to the symmetric, demisymmetric and windowed tiles there are (at least) four other order 3 6th unit cubic tiles, including two “external” tiles. As a 3 element tile potentially has 6 partial postautocomposition derivatives, 3 of order 5 and 3 of order 7, these two tiles give rise to 12 candidate attractors. However 4 of these are not connected, leaving 8 tiles - 5 order 5 tiles and 3 order 7 tiles.
The first external tile gives rise to 2 order 5 tiles and 1 order 7 tile. The order 5 tiles have the dissection polynomial c+2c2+c3+c4.


The minimal unit cells have 2 copies of the tile. When the IFS for the tile
is { p→-ap + 1;
p→-ap - 1; p→-a3p - 1 + a +
3a2 } the cell transforms for the first are { p→p; p→-ap
- 1 } and for the second are {
p→p; p→-ap + 1 },
giving a signature in both cases of 01.


The order 7 tile has the dissection polynomial 4c2+c3+2c4.

The minimal unit cell (shown below) contains 3 copies of the tile, with a
signature of 011. The cell transforms are {
p→p; p→-ap - 1;
p→-ap + 1 }.

The second external tile gives rise to 3 order 5 tiles and 2 order 7 tiles. Two order 5 tiles have the dissection polynomial c+2c2+c3+c4; the 3rd 2c+2c3+c5.



The minimal unit cells have 2 copies of the tile. When the IFS for the tile
is { p→-ap + 1;
p→-ap - 1; p→-a3p - 1 + a +
3a2 } the cell transforms for the first are { p→p; p→-ap
- 1 }, for the second {
p→p; p→-ap + 1 }, and
for the third { p→p;
p→-a3p - 1 + a + 3a2 }



The order 7 tiles have the dissection polynomials 4c2+c3+2c4 and
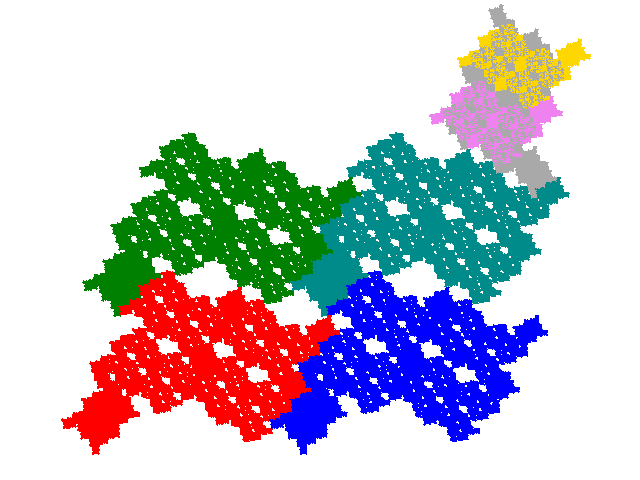

They both have 3 copies in the unit cell, with signatures 011 and 013 respectively


© 2015, 2016, 2017 Stewart R. Hinsley